题目内容
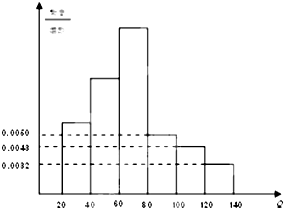 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).(1)求此次拦查中醉酒驾车的人数;
(2)驾驶人员血液中的酒精含量Q的中位数;
(3)从违法驾车的40人中按酒后驾车和醉酒驾车利用分层抽样抽取4人做样本进行研究,再从抽取的4人中任取2人,求2人中无醉酒驾车的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)求出Q>80时对应的三个矩形的纵坐标和乘以组距求出醉酒驾车的频率;再用频率乘以60求出醉酒驾车的人数.
(2)根据利用频率分布直方图估计中位数的方法,结合已知中的频率分布直方图,可得驾驶人员血液中的酒精含量Q的中位数;
(3)利用分层抽样的特点求出4人中酒后驾车和醉酒驾车的人数;利用古典概型的概率公式可得从抽取的4人中任取2人,2人中无醉酒驾车的概率.
(2)根据利用频率分布直方图估计中位数的方法,结合已知中的频率分布直方图,可得驾驶人员血液中的酒精含量Q的中位数;
(3)利用分层抽样的特点求出4人中酒后驾车和醉酒驾车的人数;利用古典概型的概率公式可得从抽取的4人中任取2人,2人中无醉酒驾车的概率.
解答:
解:(1)由已知中的频率分布直方图可得:
醉酒驾车的频率为:(0.0032+0.0043+0.0050)×20=0.25,
又由样本容量为40,故醉酒驾车的人数为:0.25×40=10,
所以此次拦查中醉酒驾车的人数为10人.…(4分)
(2)∵前两组的累积频率为:(0.0090+0.0125)×20=0.43<0.5,
前三组的累积频率为:(0.0090+0.0125+0.016)×20=0.75>0.5,
故驾驶人员血液中的酒精含量Q的中位数落在第三组,
故驾驶人员血液中的酒精含量Q的中位数约为:60+
×20=64.375…(8分)
(3)从违法驾车的40人中按酒后驾车和醉酒驾车利用分层抽样抽取4人,抽样比k=
=
,
故抽取4人中含有醉酒驾车者为10×
=1人,
从抽取的4人中任取2人共有:
=6种抽法,
其中2人中无醉酒驾车的抽法有:
=3种,
故从抽取的4人中任取2人,2人中无醉酒驾车的概率P=
=
…(12分)
醉酒驾车的频率为:(0.0032+0.0043+0.0050)×20=0.25,
又由样本容量为40,故醉酒驾车的人数为:0.25×40=10,
所以此次拦查中醉酒驾车的人数为10人.…(4分)
(2)∵前两组的累积频率为:(0.0090+0.0125)×20=0.43<0.5,
前三组的累积频率为:(0.0090+0.0125+0.016)×20=0.75>0.5,
故驾驶人员血液中的酒精含量Q的中位数落在第三组,
故驾驶人员血液中的酒精含量Q的中位数约为:60+
| 7 |
| 32 |
(3)从违法驾车的40人中按酒后驾车和醉酒驾车利用分层抽样抽取4人,抽样比k=
| 4 |
| 40 |
| 1 |
| 10 |
故抽取4人中含有醉酒驾车者为10×
| 1 |
| 10 |
从抽取的4人中任取2人共有:
| C | 2 4 |
其中2人中无醉酒驾车的抽法有:
| C | 2 3 |
故从抽取的4人中任取2人,2人中无醉酒驾车的概率P=
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查频率分布直方图中分布在某范围内的频率等于纵坐标乘以组距、考查频率等于频数除以样本容量、利用频率分布直方图估计中位数,考查古典概型,难度不大,属于基础题.

练习册系列答案
相关题目
已知f(x)=ax3+bx-4,若f(-2)=2,则f(2)=( )
| A、-2 | B、-4 | C、-6 | D、-10 |