题目内容
已知函数f(x)是定义在[-e,e]上的奇函数,当x∈(0,e]时f(x)=ax+2lnx(a∈R).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)是否存在实数a,使得当x∈[-e,0)时,函数f(x)的最小值是4?如果存在,求出a的值,如果不存在,请说明理由.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)是否存在实数a,使得当x∈[-e,0)时,函数f(x)的最小值是4?如果存在,求出a的值,如果不存在,请说明理由.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)要求f(x)解析式,需求出x∈[-e,0]上的解析式,所以设x∈[-e,0),-x∈(0,e],根据f(x)是奇函数及在(0,e]上的解析式,便可求出f(-x)=-ax+2ln(-x)=-f(x),这样即可求出f(x)在[-e,0)上的解析式,又f(0)=0,所以可以写出f(x)的解析式;
(Ⅱ)对x∈[-e,0)上的解析式求导,f′(x)=0时,x=
,所以讨论
和区间[-e,0)的关系:
≤-e,即a≤-
时,判断f′(x)在[-e,0)上的符号大于0,从而判断出函数f(x)在[-e,0)上的单调递增,f(x)的最小值为f(-e)=-ae-2=4,所以a=-
<-
,即这种情况不存在;-e<
<0,即a<-
,容易判断出x=
时f(x)取最小值f(
)=2-2ln(-
),求出a=-2e<-
,即存在a=-2e使得当x∈[-e,0)时,函数f(x)的最小值是4.
(Ⅱ)对x∈[-e,0)上的解析式求导,f′(x)=0时,x=
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| e |
| 6 |
| a |
| 2 |
| e |
| 2 |
| a |
| 2 |
| e |
| 2 |
| e |
| 2 |
| e |
| 2 |
| a |
| 2 |
| e |
解答:
解:(Ⅰ)设x∈[-e,0),则-x∈(0,e];
∴f(-x)=-ax+2ln(-x)=-f(x);
∴f(x)=ax-2ln(-x);
∵f(x)是奇函数,∴f(0)=0;
∴函数f(x)的解析式为:f(x)=
;
(Ⅱ)假设存在这样的a,使得当x∈[-e,0)时,f(x)=ax-2ln(-x)有最小值4;
∵f′(x)=a-
=
,x∈[-e,0);
①当
≤-e,即-
≤a<0,则ax-2≤0,x<0,∴f′(x)≥0;
∴f(x)是[-e,0)上的增函数,∴f(x)min=f(-e)=-ae-2=4,解得a=-
<-
,∴这种情况不存在;
②当-e<
<0,即a<-
,则x∈[-e,
)时,ax-2>0,x<0,∴f′(x)<0,x∈(
,0)时,ax-2<0,x<0,∴f′(x)>0;
∴x=
时,f(x)min=f(
)=2-2ln(-
)=4,解得 a=-2e;
综上得,存在实数a=-2e,使得当x∈[-e,0)时,f(x)的最小值是4.
∴f(-x)=-ax+2ln(-x)=-f(x);
∴f(x)=ax-2ln(-x);
∵f(x)是奇函数,∴f(0)=0;
∴函数f(x)的解析式为:f(x)=
|
(Ⅱ)假设存在这样的a,使得当x∈[-e,0)时,f(x)=ax-2ln(-x)有最小值4;
∵f′(x)=a-
| 2 |
| x |
| ax-2 |
| x |
①当
| 2 |
| a |
| 2 |
| e |
∴f(x)是[-e,0)上的增函数,∴f(x)min=f(-e)=-ae-2=4,解得a=-
| 6 |
| e |
| 2 |
| e |
②当-e<
| 2 |
| a |
| 2 |
| e |
| 2 |
| a |
| 2 |
| a |
∴x=
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
综上得,存在实数a=-2e,使得当x∈[-e,0)时,f(x)的最小值是4.
点评:考查求函数解析式的方法,奇函数的定义,函数导数符号和函数单调性的关系,函数最值的概念及求法.

练习册系列答案
相关题目
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:
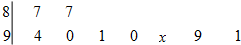
则7个剩余分数的方差为( )
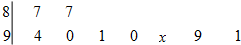
则7个剩余分数的方差为( )
A、
| ||||
B、
| ||||
| C、36 | ||||
D、
|
设M(5,-1,2),A(4,2,-1),O(0,0,0),若
=
,则点B的坐标应为( )
| OM |
| AB |
| A、(-1,3,-3) |
| B、(1,-3,3) |
| C、(9,1,1) |
| D、(-9,-1,-1) |
过点P(-4,0)的直线l与曲线C:x2+2y2=4交于A,B两点;则AB中点Q的轨迹方程为( )
| A、(x+2)2+2y2=4 |
| B、(x+2)2+2y2=4(-1<x≤0) |
| C、x2+2(y+2)2=4 |
| D、x2+2(y+2)2=4(-1<x≤0) |
判断方程(
)x=x2的根的个数是( )
| 1 |
| 2 |
| A、4个 | B、3个 | C、2个 | D、1个 |
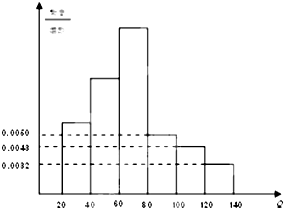 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).