题目内容
利用f(2)=2-X的图象做出f(x-1)的图象,并写出作图步骤.
考点:指数函数的图像变换
专题:函数的性质及应用
分析:f(x-1)的图象可由f(x)的图象向右平移一个单位得到,结合指数函数的图象和性质,及函数图象的平移变换,可得答案.
解答:
解:f(x-1)的图象可由f(x)的图象向右平移一个单位得到,
要得到f(x-1)的图象其步骤为:
①先根据指数的运算性质,得到f(x)=2-X=(
)X,
②根据指数函数的图象和性质,画出f(x)的图象C,
③将C向右平移一个单位,得到f(x-1)的图象.
如下图所示:

要得到f(x-1)的图象其步骤为:
①先根据指数的运算性质,得到f(x)=2-X=(
| 1 |
| 2 |
②根据指数函数的图象和性质,画出f(x)的图象C,
③将C向右平移一个单位,得到f(x-1)的图象.
如下图所示:

点评:本题考查的知识点是函数图象的平移变换,指数函数的图象和性质,难度不大,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
方程x=2+log
x的根所在的区间是( )
| 1 |
| 2 |
| A、(1,2) |
| B、(0,1) |
| C、(2,3) |
| D、(4,5) |
判断方程(
)x=x2的根的个数是( )
| 1 |
| 2 |
| A、4个 | B、3个 | C、2个 | D、1个 |
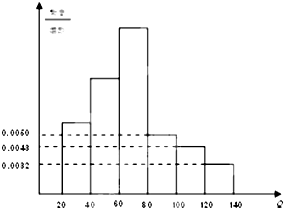 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).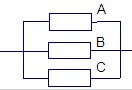 如图,在一段线路中并联着3个自动控制的开关,只要其中有一个开关能够闭合,线路就正常工作,假在某段时间内每个开关能够闭合的概率是0.5,请你用树状图求出在这段时间内正常工作的概率.
如图,在一段线路中并联着3个自动控制的开关,只要其中有一个开关能够闭合,线路就正常工作,假在某段时间内每个开关能够闭合的概率是0.5,请你用树状图求出在这段时间内正常工作的概率.