题目内容
过点P(1,4)作直线l,直线l与x,y的正半轴分别交于A,B两点,O为原点,
(Ⅰ)△ABO的面积为9,求直线l的方程;
(Ⅱ)若△ABO的面积为S,求S的最小值并求此时直线l的方程.
(Ⅰ)△ABO的面积为9,求直线l的方程;
(Ⅱ)若△ABO的面积为S,求S的最小值并求此时直线l的方程.
考点:直线的截距式方程
专题:直线与圆
分析:(Ⅰ)由点P设出直线l的方程,求出l与x、y轴的交点坐标,由△的面积求出斜率k的值即可;
(Ⅱ)由△ABO的面积S表达式,用基本不等式求出k的值,即得l的方程.
(Ⅱ)由△ABO的面积S表达式,用基本不等式求出k的值,即得l的方程.
解答:
解:(Ⅰ)设直线l为:y-4=k(x-1),
即y=kx-k+4(k<0);
∴直线l与x轴和y轴的交点坐标分别为:
(1-
,0),(0,4-k);
∴△ABO的面积为:
(4-k)(1-
)=9,
解得k=-2或k=-8;
∴直线l为:2x+y-6=0或8x+y-12=0.
(Ⅱ)由(1)知,△ABO的面积为:
S=
(4-k)(1-
)=
(8-k-
)≥
(8+8)=8;
当且仅当-k=-
,即k=-4时,“=”成立,
∴k=-4时,直线l为:4x+y-8=0.
即y=kx-k+4(k<0);
∴直线l与x轴和y轴的交点坐标分别为:
(1-
| 4 |
| k |
∴△ABO的面积为:
| 1 |
| 2 |
| 4 |
| k |
解得k=-2或k=-8;
∴直线l为:2x+y-6=0或8x+y-12=0.
(Ⅱ)由(1)知,△ABO的面积为:
S=
| 1 |
| 2 |
| 4 |
| k |
| 1 |
| 2 |
| 16 |
| k |
| 1 |
| 2 |
当且仅当-k=-
| 16 |
| k |
∴k=-4时,直线l为:4x+y-8=0.
点评:本题考查了平面内直线方程的应用以及基本不等式的应用问题.

练习册系列答案
相关题目
已知函数f(x)=ax5+bx3+cx-2,且f (-12)=10,则f(12)=( )
| A、-14 | B、-12 |
| C、-10 | D、10 |
已知空间4个球,它们的半径均为2,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
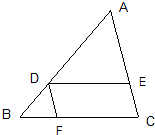 (几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=
(几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=