Question

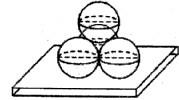
已知空间4个球，它们的半径均为2，每个球都与其他三个球外切，另有一个小球与这4个球都外切，则这个小球的半径为（　　）

• A、

  6

  -2
• B、

  6

  -

  2

• C、

  10

  -3
• D、2

  2

  -2

Answer 1

考点：球的体积和表面积

专题：空间位置关系与距离

分析：将这四个球的球心连接成一个正四面体，并根据四球外切，得到四面体的棱长为2，求出外接球半径，由于这四个球之间有一个小球和这四个球都外切，则小球的球心与四面体的球体重合，进而再由小球与其它四球外切，球心距（即正四面体外接球半径）等于大球半径与小球半径之和，得到答案．

解答： 解：连接四个球的球心，得到一个棱长为4的正四面体，则该正四面体的外接球半径为

6

，
若这四个球之间有一个小球和这四个球都外切，则小球的球心与四面体的球体重合，
因为由小球与其它四球外切，所以球心距（即正四面体外接球半径）等于大球半径与小球半径之和，
所以所求小球的半径为

6

-2．
故选A．

点评：本题考查棱锥的结构特征，球的结构特征，其中根据已知条件求出四个半径为1的球球心连接后所形成的正四面体的棱长及外接球半径的长是解答本题的关键．