题目内容
若f(x)的定义域为R,若对任意不等实数x1、x2满足
<0,且对任意x、y∈R,f(x2-2x)+f(2y-y2)≤0恒成立,又f (x-1)的图象关于(1,0)对称.则当1≤x≤4,
的取值范围是 .
| f(x1)-f(x2) |
| x1-x2 |
| y |
| x |
考点:函数恒成立问题
专题:计算题,函数的性质及应用
分析:由
<0,可得:函数f(x)是递减函数.由函数y=f(x-1)的图象关于点(1,0)对称,可得函数f(x)是奇函数,再结合f(x2-2x)+f(2y-y2)≤0可得(x-y)(x+y-2)≥0(1≤x≤4),
进而利用线性规划的知识解决问题.
| f(x1)-f(x2) |
| x1-x2 |
进而利用线性规划的知识解决问题.
解答:
解:因为对任意不等实数x1,x2满足
<0,
所以函数f(x)是定义在R上的单调递减函数.
因为函数y=f(x-1)的图象关于点(1,0)对称,
所以函数y=f(x)的图象关于点(0,0)对称,即函数f(x)是定义在R上的奇函数.
又因为对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,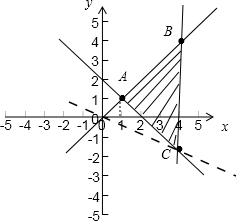
所以f(x2-2x)≤f(-2y+y2)成立,
所以根据函数的单调性可得:对于任意的x,y∈R,不等式x2-2x≥y2-2y成立,
即(x-y)(x+y-2)≥0(1≤x≤4),
所以可得其可行域,如图所示:
因为
=
,
所以
表示点(x,y)与点(0,0)连线的斜率,
所以结合图象可得:
的最小值是直线OC的斜率-
,最大值是直线AB的斜率1,
所以
的范围为:[-
,1].
故答案为:[-
,1].
| f(x1)-f(x2) |
| x1-x2 |
所以函数f(x)是定义在R上的单调递减函数.
因为函数y=f(x-1)的图象关于点(1,0)对称,
所以函数y=f(x)的图象关于点(0,0)对称,即函数f(x)是定义在R上的奇函数.
又因为对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,

所以f(x2-2x)≤f(-2y+y2)成立,
所以根据函数的单调性可得:对于任意的x,y∈R,不等式x2-2x≥y2-2y成立,
即(x-y)(x+y-2)≥0(1≤x≤4),
所以可得其可行域,如图所示:
因为
| y |
| x |
| y-0 |
| x-0 |
所以
| y |
| x |
所以结合图象可得:
| y |
| x |
| 1 |
| 2 |
所以
| y |
| x |
| 1 |
| 2 |
故答案为:[-
| 1 |
| 2 |
点评:解决此类问题的关键是熟练掌握抽象函数的性质的证明与判断,如单调性、奇偶性的证明与判断,并且熟练的利用函数的性质解有关的不等式,以及熟练掌握线性规划问题,此题综合性较强知识点也比较零散,对学生掌握知识与运用知识的能力有一定的要求.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
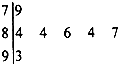 如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、84,4.84 |
| B、84,1.6 |
| C、85,1.6 |
| D、85,4 |
点P是双曲线
-
=1(a>0,b>0)左支上的点,右焦点为F(c,0),若M为线段FP的中点,且M到原点的距离为
,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 8 |
A、(1,
| ||||
| B、(1,8] | ||||
C、(
| ||||
| D、(2,3] |
数列{xn}对任意n∈N*满足(1+xn)(1-xn+1)=2,且x1=2,则x2015的值为( )
| A、-3 | ||
| B、-2 | ||
| C、2 | ||
D、-
|
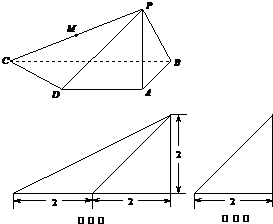 四棱锥P-ABCD的直观图、主视图、侧视图如图所示,主视图是直角三角形,侧视图是等腰直角三角形,有关数据如图所示.
四棱锥P-ABCD的直观图、主视图、侧视图如图所示,主视图是直角三角形,侧视图是等腰直角三角形,有关数据如图所示.