题目内容
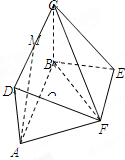如图，矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直，已知四边形ABEF为等腰梯形，点O为AB的中点，M为CD的中点，AB∥EF，AB=2，AF=EF=1．（1）求证：平面DAF⊥平面CBF；
（2）若直线AM与平面CBF所成角的正弦值为
| ||
| 10 |
考点：直线与平面所成的角,平面与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）根据面面垂直的判定定理即可证明平面DAF⊥平面CBF；
（2）根据线面所成的角的定义建立条件关系即可求AD的长
（2）根据线面所成的角的定义建立条件关系即可求AD的长
解答：
解：（1）过F作FG⊥AB，
∵四边形ABEF为等腰梯形，且AB=2，AF=EF=1，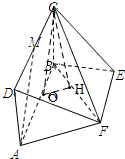
∴AG=
，∠BAF=60°，
∵余弦定理得BF=
，
∴AF2+BF2=AB2，
即AF⊥BF，
∵矩形ABCD，∴BC⊥AB，
∵面ABCD⊥面ABEF，面ABCD∩面ABEF=AB，
∴BC⊥平面ABEF，
∵AF?平面ABEF，∴AF⊥BC，
∵BF∩BC=B，
∴AF⊥面CBF，
∵AF⊥面DAF，
∴平面DAF⊥平面CBF
（2）连结OC，则AM∥OC，
则直线OC与平面CBF所成的角即可为直线AM与CBF所成的角，
取BF的中点H，连结OH，
∵O，H分别是AB，BF的中点，∴OH∥AF，
由（1）知，AF⊥面CBF，
∴OH⊥面CBF，
即∠OCH即为所求角，
设AD=t，则OC=AM=
，
则sin∠OCH=
=
=
，解得t=2，
∴AD=2．
∵四边形ABEF为等腰梯形，且AB=2，AF=EF=1，
∴AG=
| 1 |
| 2 |
∵余弦定理得BF=
| 3 |
∴AF2+BF2=AB2，
即AF⊥BF，
∵矩形ABCD，∴BC⊥AB，
∵面ABCD⊥面ABEF，面ABCD∩面ABEF=AB，
∴BC⊥平面ABEF，
∵AF?平面ABEF，∴AF⊥BC，
∵BF∩BC=B，
∴AF⊥面CBF，
∵AF⊥面DAF，
∴平面DAF⊥平面CBF
（2）连结OC，则AM∥OC，
则直线OC与平面CBF所成的角即可为直线AM与CBF所成的角，
取BF的中点H，连结OH，
∵O，H分别是AB，BF的中点，∴OH∥AF，
由（1）知，AF⊥面CBF，
∴OH⊥面CBF，
即∠OCH即为所求角，
设AD=t，则OC=AM=
| 1+t2 |
则sin∠OCH=
| OH |
| OC |
| ||
|
| ||
| 10 |
∴AD=2．
点评：本题主要考查面面垂直的判定以及线面所成角的定义，要求熟练掌握常见的定理，综合性较强．
练习册系列答案
相关题目
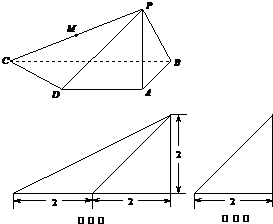四棱锥P-ABCD的直观图、主视图、侧视图如图所示，主视图是直角三角形，侧视图是等腰直角三角形，有关数据如图所示．