题目内容
3.若x,y满足$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$,则z=2x+y的最小值是( )| A. | $\frac{20}{3}$ | B. | 8 | C. | $\frac{14}{3}$ | D. | 5 |
分析 画出满足约束条件的可行域,利用目标函数的几何意义,判断目标函数经过的点,可得最优解.
解答  解:满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$的可行域如下图所示:
解:满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$的可行域如下图所示:
∵目标函数z=2x+y,平移目标函数,当目标函数经过可行域的点A时,取得最小值.$\left\{\begin{array}{l}{x-2y=0}\\{x+2y=4}\end{array}\right.$,可得A(2,1)
故在A(2,1)处目标函数达到最小值:5.
故选:D.
点评 本题考查的知识点是简单线性规划,掌握目标函数的几何意义,熟练掌握其解答过程和步骤是解答的关键.

练习册系列答案
相关题目
14.为了得到函数y=1-2sin2(x-$\frac{π}{12}$)的图象,可以将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
8.正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则AD1与平面BB1D1所成角的正弦值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
12.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则直线AB的方程是( )
| A. | x+3y=0 | B. | 3x-y=0 | C. | 3x-y-9=0 | D. | 3x+y+9=0 |
13.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/10kg)与上市时间t(单位:元)的数据如表:
(1)根据上表数据判断,函数Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt中哪一个适宜作为描述西红柿种植成本Q与上市时间t的变化关系?简要说明理由;
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
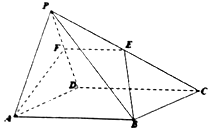 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.