题目内容
11.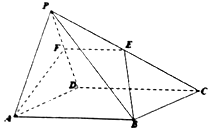 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.
分析 (1)证明CD∥EF,AB∥CD,即可证明AB∥EF,利用线面平行的判定即可得解;
(2)利用平面PAD⊥平面ABCD,证明CD⊥AF,PA=AD,所以AF⊥PD,即可证明AF⊥平面PCD;
解答 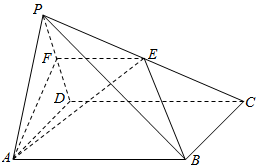 (本题满分为12分)
(本题满分为12分)
解:(1)证明:因为点E、F分别是棱PC和PD的中点,
所以CD∥EF.
因为底面ABCD是矩形,
所以AB∥CD.可得:AB∥EF,
又因为EF?平面PAB,AB?平面PAB,
所以EF∥平面PAB.…(6分)
(2)证明:在矩形ABCD中,CD⊥AD.
又因为平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
所以CD⊥平面PAD.
又AF?平面PAD,
所以CD⊥AF.
由点F是棱PD中点.
在△PAD中,因为PA=AD,所以AF⊥PD.
又因为PD∩CD=D,所以AF⊥平面PCD.…(12分)
点评 本题考查线面平行的性质,平面与平面垂直的性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
1.已知实数a>0,b>0,若2a+b=1,则$\frac{1}{a}+\frac{2}{b}$的最小值是( )
| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | 4 | D. | 8 |
2.曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1与曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的( )
| A. | 实轴长相等 | B. | 离心率相等 | C. | 范围相同 | D. | 渐近线相同 |
6.在△ABC中,三个内角A、B、C成等差数列,且cosA=$\frac{2}{3}$,则sinC=( )
| A. | $\frac{-2\sqrt{3}+\sqrt{5}}{6}$ | B. | $\frac{2\sqrt{3}+\sqrt{5}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{5}}{6}$ | D. | $\frac{-2\sqrt{3}-\sqrt{5}}{6}$ |
3.若x,y满足$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$,则z=2x+y的最小值是( )
| A. | $\frac{20}{3}$ | B. | 8 | C. | $\frac{14}{3}$ | D. | 5 |
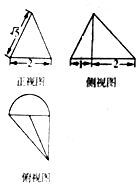 某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.