题目内容
8.正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则AD1与平面BB1D1所成角的正弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 建立空间直角坐标系,求出平面的法向量,利用向量法即可求AD1与面BB1D1D所成角的正弦值.
解答 解:以D为原点,DA,DC,DD1分别为x轴,y轴,z轴,建立如图所示空间直角坐标系D-xyz.
设AB=1,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,0,2),
A1(1,0,2),B1(1,1,2),C1(0,1,2).
设AD1与面BB1D1D所成角的大小为θ,$\overrightarrow{A{D}_{1}}$=(-1,0,2),
设平面BB1D1D的法向量为$\overrightarrow{n}$=(x,y,z),$\overrightarrow{DB}$=(1,1,0),$\overrightarrow{D{D}_{1}}$=(0,0,2),
则x+y=0,z=0.
令x=1,则y=-1,所以$\overrightarrow{n}$=(1,-1,0),
sinθ=|cos<$\overrightarrow{A{D}_{1}}$,$\overrightarrow{n}$>|=$\frac{\sqrt{10}}{10}$,
所以AD1与平面BB1D1D所成角的正弦值为$\frac{\sqrt{10}}{10}$.
故选:A.
点评 本题主要考查直线和平面所成角的求解,建立坐标系,利用向量法是解决空间角的常用方法.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
3.若x,y满足$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$,则z=2x+y的最小值是( )
| A. | $\frac{20}{3}$ | B. | 8 | C. | $\frac{14}{3}$ | D. | 5 |
17.过圆C:(x-4)2+(y+1)2=25上的点M(0,2)作其切线l,且与直线l′:4x-ay+2=0平行,则l′与l间的距离是( )
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |
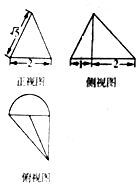 某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.