题目内容

13．表面积为20π的球面上有四点S、A、B、C，且△ABC是边长为2$\sqrt{3}$的等边三角形，若平面SAB⊥平面ABC，则三棱锥S-ABC体积的最大值是3$\sqrt{3}$．

分析 作出直观图，根据球和等边三角形的性质计算△SAB的面积和棱锥的最大高度，代入体积公式计算．

解答 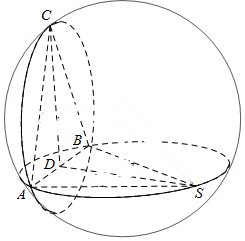解：取AB中点D，连结SD，设球O半径为r，则4πr2=20π，
解得r=$\sqrt{5}$，△ABC是边长为2$\sqrt{3}$的等边三角形，AB=2$\sqrt{3}$，CD=3．AD=$\sqrt{3}$，
过S作ABC的垂线，垂足是AB的中点时，
所求三棱锥的体积最大，此时△SAB与△ABC全等，SD=3，
三棱锥S-ABC体积V=$\frac{1}{3}$S△SAB•CD=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×（2$\sqrt{3}$）2×3=3$\sqrt{3}$．
故答案为：3$\sqrt{3}$．

点评 本题考查了棱锥的体积计算，空间几何体的作图能力，准确画出直观图找到棱锥的最大高度是解题关

练习册系列答案
相关题目
3．已知1＜m＜4，F1，F2为曲线$C：\frac{x^2}{4}+\frac{y^2}{4-m}=1$的左、右焦点，点P为曲线C与曲线$E：{x^2}-\frac{y^2}{m-1}=1$在第一象限的交点，直线l为曲线C在点P处的切线，若三角形F1PF2的内心为点M，直线F1M与直线l交于N点，则点M，N横坐标之和为（　　）
A．1B．2C．3D．随m的变化而变化
4．已知四棱锥P-ABCD的直观图与三视图如图所示，其中正（主）视图与侧（左）视图为直角三角形，俯视图为正方形（数据如图所示），已知该几何体的体积为$\frac{2}{3}$．
（1）求实数a的值；
（2）将△PAB绕PB旋转一周，求所得旋转体的体积．
1．已知实数a＞0，b＞0，若2a+b=1，则$\frac{1}{a}+\frac{2}{b}$的最小值是（　　）
A．$\frac{8}{3}$B．$\frac{11}{3}$C．4D．8
8．在Rt△AOB中，$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，|$\overrightarrow{OA}$|=$\sqrt{5}$，|$\overrightarrow{OB}$|=2$\sqrt{5}$，AB边上的高为OD，D在AB上，点E位于线段OD上，若$\overrightarrow{OE}$•$\overrightarrow{EA}$=$\frac{3}{4}$，则向量$\overrightarrow{EA}$在向量$\overrightarrow{OD}$上的投影为（　　）
A．$\frac{1}{2}$或$\frac{3}{2}$B．1C．1或$\frac{1}{2}$D．$\frac{3}{2}$
18．命题“?x∈R，x2＞9”的否定是?x∈R，x2≤9．
5．已知函数f（x）=a（x-1）-lnx（a为实数），g（x）=x-1，h（x）=$\left\{\begin{array}{l}g（x），f（x）＜g（x）\\ f（x），f（x）≥g（x）\end{array}$．
（1）当a=1时，求函数f（x）=a（x-1）-lnx在点（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性；
（3）若h（x）=f（x），求实数a的值．
2．曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1与曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的（　　）
A．实轴长相等B．离心率相等C．范围相同D．渐近线相同
3．若x，y满足$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$，则z=2x+y的最小值是（　　）
A．$\frac{20}{3}$B．8C．$\frac{14}{3}$D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网