题目内容
14.为了得到函数y=1-2sin2(x-$\frac{π}{12}$)的图象,可以将函数y=sin2x的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
分析 根据诱导公式,二倍角的余弦函数公式化简可得函数解析式y=sin[2(x+$\frac{π}{6}$)],再利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:∵y=1-2sin2(x-$\frac{π}{12}$)=cos(2x-$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$)=sin[2(x+$\frac{π}{6}$)],
故把函数y=sin2x的图象向左平移$\frac{π}{6}$个单位可得函数y=cos2(x+$\frac{π}{6}$)=1-2sin2(x-$\frac{π}{12}$)的图象,
故选:D.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.

练习册系列答案
相关题目
2.曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1与曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的( )
| A. | 实轴长相等 | B. | 离心率相等 | C. | 范围相同 | D. | 渐近线相同 |
9.下列命题成立的是( )
| A. | 若¬p、¬q均为真命题,则p∨q为真命题 | |
| B. | 命题“若x2+2x<0,则-2<x<0”的逆否命题为“若-2<x<0,则x2+2x<0” | |
| C. | 方程x2=1的一个必要不充分条件是x=1 | |
| D. | 抛掷3枚质地均匀的硬币,事件“至少有两枚硬币正面向上”等价于“至多有一枚硬币反面向上” |
6.在△ABC中,三个内角A、B、C成等差数列,且cosA=$\frac{2}{3}$,则sinC=( )
| A. | $\frac{-2\sqrt{3}+\sqrt{5}}{6}$ | B. | $\frac{2\sqrt{3}+\sqrt{5}}{6}$ | C. | $\frac{2\sqrt{3}-\sqrt{5}}{6}$ | D. | $\frac{-2\sqrt{3}-\sqrt{5}}{6}$ |
3.若x,y满足$\left\{\begin{array}{l}{x+y≤4}\\{x-2y≥0}\\{x+2y≥4}\end{array}\right.$,则z=2x+y的最小值是( )
| A. | $\frac{20}{3}$ | B. | 8 | C. | $\frac{14}{3}$ | D. | 5 |
4. 如图,在三棱锥C-DAB中,E,F分别是AC,BD的中点,若EF⊥AB,且向量$\overrightarrow{EF}$与$\overrightarrow{CD}$的夹角为30°,则棱CD与棱AB的关系是( )
如图,在三棱锥C-DAB中,E,F分别是AC,BD的中点,若EF⊥AB,且向量$\overrightarrow{EF}$与$\overrightarrow{CD}$的夹角为30°,则棱CD与棱AB的关系是( )
 如图,在三棱锥C-DAB中,E,F分别是AC,BD的中点,若EF⊥AB,且向量$\overrightarrow{EF}$与$\overrightarrow{CD}$的夹角为30°,则棱CD与棱AB的关系是( )
如图,在三棱锥C-DAB中,E,F分别是AC,BD的中点,若EF⊥AB,且向量$\overrightarrow{EF}$与$\overrightarrow{CD}$的夹角为30°,则棱CD与棱AB的关系是( )| A. | CD=2AB | B. | CD=AB | C. | AB=2CD | D. | 无法确定 |
 已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.
已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.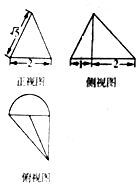 某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.