题目内容
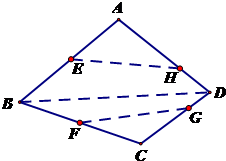如图，在空间四边形ABCD中，E，F分别是AB和CB上的点，G，F分别是CD和AD上的点，且
| AE |
| EB |
| CF |
| FB |
| AH |
| HD |
| CG |
| GD |
考点：平面的基本性质及推论
专题：证明题,空间位置关系与距离
分析：先证P为两个平面的公共点，利用两个平面的公共点在两个平面的公共直线上，证线共点．
解答：
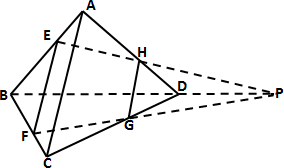解：连接EF，GH，
因为
=
=1，
=
=2，
所以EF∥AC，HG∥AC且EF≠AC …（2分）
所以EH，FG共面，且EH与FG不平行，…（3分）
不妨设EH∩FG=P …（4分）
则P∈EH，EH?面ABD，
所以P∈面ABD；…（6分）
同理P∈面BCD…（8分）
又因为平面ABD∩平面BCD=BD，所以P∈BD，…（10分）
所以EH，BD，FG三条直线相交于同一点P．…（12分）
解：连接EF，GH，因为
| AE |
| EB |
| CF |
| FB |
| AH |
| HD |
| CG |
| GD |
所以EF∥AC，HG∥AC且EF≠AC …（2分）
所以EH，FG共面，且EH与FG不平行，…（3分）
不妨设EH∩FG=P …（4分）
则P∈EH，EH?面ABD，
所以P∈面ABD；…（6分）
同理P∈面BCD…（8分）
又因为平面ABD∩平面BCD=BD，所以P∈BD，…（10分）
所以EH，BD，FG三条直线相交于同一点P．…（12分）
点评：本题考查了用公理2证明点共线问题，考查平行关系的转化，考查了学生的空间想象能力和推理论证能力，本题较好的体现了线线、线面平行关系的转化．
练习册系列答案
阅读快车系列答案
相关题目
函数y=2x+sinx的单调增区间是（ ）
| A、（-∞，+∞） | ||||
| B、（0，+∞） | ||||
C、（2kπ-
| ||||
| D、以上答案均不正确 |