题目内容
设数列{an}的前n项和为Sn,d为常数,已知对?n,m∈N*,当n>m,总有Sn-Sm=Sn-m+m(n-m)d成立
(1)求证:数列{an}是等差数列;
(2)若正整数n,m,k成等差数列,比较Sn+Sk与2Sm的大小,并说明理由;
(3)探究:命题p:“对?n,m∈N*,当n>m时,总有Sn-Sm=Sn-m+m(n-m)d”是命题q:“数列{an}是等差数列”的充要条件吗?请证明你的结论;由此类比,请你写出数列{bn}是等比数列(公比为q,且q≠0)的充要条件(无需证明)?
(1)求证:数列{an}是等差数列;
(2)若正整数n,m,k成等差数列,比较Sn+Sk与2Sm的大小,并说明理由;
(3)探究:命题p:“对?n,m∈N*,当n>m时,总有Sn-Sm=Sn-m+m(n-m)d”是命题q:“数列{an}是等差数列”的充要条件吗?请证明你的结论;由此类比,请你写出数列{bn}是等比数列(公比为q,且q≠0)的充要条件(无需证明)?
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)在数列递推式中,取m=n-1,得到an=a1+(n-1)d (n≥2),验证n=1时成立,从而证得数列{an}是等差数列;
(2)由等差数列的前n项和求得Sn,Sk,Sm,然后利用作差法得到Sn+Sk-2Sm=
(n-k)2,对d分类讨论得答案;
(3)由(1)的证明得到充分性,由等差数列的性质结合前n项和再证必要性,则说明结论成立,然后直接写出数列{bn}是等比数列(公比为q,且q≠0)的充要条件.
(2)由等差数列的前n项和求得Sn,Sk,Sm,然后利用作差法得到Sn+Sk-2Sm=
| d |
| 4 |
(3)由(1)的证明得到充分性,由等差数列的性质结合前n项和再证必要性,则说明结论成立,然后直接写出数列{bn}是等比数列(公比为q,且q≠0)的充要条件.
解答:
(1)证明:∵当n>m时,总有Sn-Sm=Sn-m+m(n-m)d成立,
∴当n≥2时,Sn-Sn-1=S1+(n-1)d,即an=a1+(n-1)d,且n=1也成立,
∴当n≥2时,an-an-1=[a1+(n-1)d]-[a1+(n-2)d=d.
∴数列{an}是等差数列;
(2)解:∵正整数n,m,k成等差数列,
∴n+k=2m,
∴Sn+Sk-2Sm=na1+
d+ka1+
d-2(ma1+
d)
=
(n2+k2-2m2)=
(n2+k2-2(
)2)=
(n-k)2.
∴①当d>0时,Sn+Sk>2Sm;
②当d<0时,Sn+Sk<2Sm;
③当d=0时,Sn+Sk=2Sm;
(3)由(1)充分性已经得证,下面证必要性.
∵数列{an}是等差数列,
∴当n>m时,
Sn-Sm-Sn-m=am+1+am+2+…+an-Sn-m
=(n-m)am+1+
d-[(n-m)a1+
d]
=(n-m)(am+1-a1)=m(n-m)d.
∴Sn-Sm=Sn-m+m(n-m)d.
∴p:“对?n,m∈N*,当n>m时,总有Sn-Sm=Sn-m+m(n-m)d”是命题q:“数列{an}是等差数列”的充要条件;
“数列{bn}是等比数列(公比为q,且q≠0)”的充要条件是“对,当n>m时,
总有Sn-Sm=qm•Sn-m.
∴当n≥2时,Sn-Sn-1=S1+(n-1)d,即an=a1+(n-1)d,且n=1也成立,
∴当n≥2时,an-an-1=[a1+(n-1)d]-[a1+(n-2)d=d.
∴数列{an}是等差数列;
(2)解:∵正整数n,m,k成等差数列,
∴n+k=2m,
∴Sn+Sk-2Sm=na1+
| n(n-1) |
| 2 |
| k(k-1) |
| 2 |
| m(m-1) |
| 2 |
=
| d |
| 2 |
| d |
| 2 |
| n+k |
| 2 |
| d |
| 4 |
∴①当d>0时,Sn+Sk>2Sm;
②当d<0时,Sn+Sk<2Sm;
③当d=0时,Sn+Sk=2Sm;
(3)由(1)充分性已经得证,下面证必要性.
∵数列{an}是等差数列,
∴当n>m时,
Sn-Sm-Sn-m=am+1+am+2+…+an-Sn-m
=(n-m)am+1+
| (n-m)(n-m-1) |
| 2 |
| (n-m)(n-m-1) |
| 2 |
=(n-m)(am+1-a1)=m(n-m)d.
∴Sn-Sm=Sn-m+m(n-m)d.
∴p:“对?n,m∈N*,当n>m时,总有Sn-Sm=Sn-m+m(n-m)d”是命题q:“数列{an}是等差数列”的充要条件;
“数列{bn}是等比数列(公比为q,且q≠0)”的充要条件是“对,当n>m时,
总有Sn-Sm=qm•Sn-m.
点评:本题考查数列递推式,考查了数列的前n项和,训练了充要条件的证明方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知2a+1<0,关于x的不等式x2-4ax-5a2>0的解集是( )
| A、{x|x>5a或x<-a} |
| B、{x|-a<x<5a} |
| C、{x|x<5a或x>-a} |
| D、{x|5a<x<-a} |
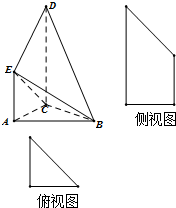 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.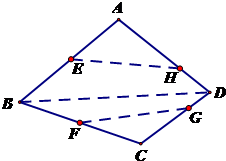 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是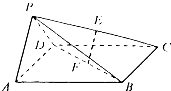 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.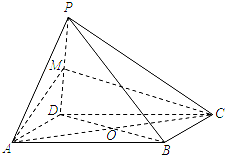 如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.
如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.