题目内容
已知函数f(x)=3x-2,数列{an}的前n项和为Sn,且点(an,2Sn)在函数y=f(x)的图象上;
(1)求数列{an}的通项公式;
(2)设bn=f(an),数列{bn}的前n项和为Tn,若
<an+1+t对任意的n∈N*恒成立,求实数t的取值范围.
(1)求数列{an}的通项公式;
(2)设bn=f(an),数列{bn}的前n项和为Tn,若
| T2n+4n |
| Tn+2n |
考点:数列与函数的综合,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)利用f(x)=3x-2,数列{an}的前n项和为Sn,且点(an,2Sn)在函数y=f(x)的图象上,可得2Sn=3an-2,再写一式,两式相减,可得{an}是首项为2,公比为3的等比数列,即可求数列{an}的通项公式;
(2)求出数列{bn}的前n项和为Tn,
<an+1+t对任意的n∈N*恒成立,转化为3n+1<2•3n+t对任意的n∈N*恒成立,即可求出实数t的取值范围.
(2)求出数列{bn}的前n项和为Tn,
| T2n+4n |
| Tn+2n |
解答:
解:(1)∵f(x)=3x-2,数列{an}的前n项和为Sn,且点(an,2Sn)在函数y=f(x)的图象上,
∴2Sn=3an-2①…(1分)
当n=1时,2S1=3a1-2,∴a1=2 …(2分)
当n≥2时,2Sn-1=3an-1-2②…(3分)
①-②有:an=3an-1 …(5分)
∴{an}是首项为2,公比为3的等比数列,
∴an=2•3n-1.…(6分)
(2)bn=f(an)=2•3n-2. …(7分)
∴Tn=2(3+32+…+3n)-2n=3n+1-2n-3. …(9分)
∴
=
=3n+1 …(11分)
∵
<an+1+t对任意的n∈N*恒成立,
∴3n+1<2•3n+t对任意的n∈N*恒成立,
即t>(-3n+1)max. …(12分)
∴t>-2. …(14分)
∴2Sn=3an-2①…(1分)
当n=1时,2S1=3a1-2,∴a1=2 …(2分)
当n≥2时,2Sn-1=3an-1-2②…(3分)
①-②有:an=3an-1 …(5分)
∴{an}是首项为2,公比为3的等比数列,
∴an=2•3n-1.…(6分)
(2)bn=f(an)=2•3n-2. …(7分)
∴Tn=2(3+32+…+3n)-2n=3n+1-2n-3. …(9分)
∴
| T2n+4n |
| Tn+2n |
| (3n-1)(3n+1) |
| 3n-1 |
∵
| T2n+4n |
| Tn+2n |
∴3n+1<2•3n+t对任意的n∈N*恒成立,
即t>(-3n+1)max. …(12分)
∴t>-2. …(14分)
点评:本题考查数列通项与求和,考查恒成立问题,体现了数列的函数特性,同时考查了运算能力,属中档题.

练习册系列答案
相关题目
现有60件产品,编号从1到60,若用系统抽样方法从中抽取6件检验,则所抽到的个体编号可能是( )
| A、5,10,15,20,25,30 |
| B、2,14,26,28,42,56 |
| C、5,8,31,36,48,54 |
| D、3,13,23,33,43,53 |
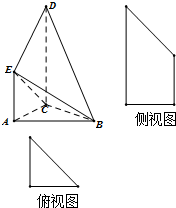 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.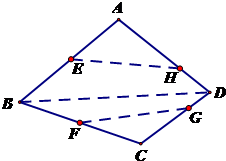 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是