题目内容
若复数z1=a+2i（a∈R），z2=3-4i，且
为纯虚数，求|z1|．
| z1 |
| z2 |
考点：复数代数形式的乘除运算
专题：计算题,数系的扩充和复数
分析：先化简
，由纯虚数的定义可得a值，进而可求|z1|．
| z1 |
| z2 |
解答：
解：
=
=
=
，
∵
为纯虚数，
∴
=0，
≠0，解得a=
，
∴|z1|=
=
=
，
|z1|=
．
| z1 |
| z2 |
| a+2i |
| 3-4i |
| (a+2i)(3+4i) |
| (3-4i)(3+4i) |
| 3a-8+(4a+6)i |
| 25 |
∵
| z1 |
| z2 |
∴
| 3a-8 |
| 25 |
| 4a+6 |
| 25 |
| 8 |
| 3 |
∴|z1|=
(
|
|
| 10 |
| 3 |
|z1|=
| 10 |
| 3 |
点评：该题考查复数代数形式的除法运算及基本概念，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
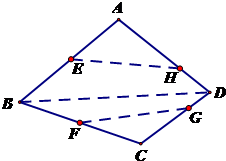如图，在空间四边形ABCD中，E，F分别是AB和CB上的点，G，F分别是
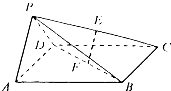如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，PA⊥PD，E、F分别为PC、BD的中点．
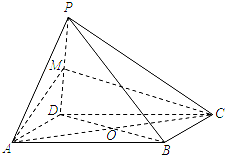如图，四棱锥P-ABCD中，O为菱形ABCD对角线的交点，M为棱PD的中点，MA=MC．