题目内容
袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是
.
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
| 7 |
| 9 |
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
考点:离散型随机变量及其分布列,古典概型及其概率计算公式
专题:概率与统计
分析:(1)设黑球的个数为x,则白球的个数为10-x,记两个都是黑球得的事件为A,则至少有一个白球的事件与事件A为对立事件,由此能求出白球的个数.
(2)离散型随机变量X的取值可能为:0,1,2,3,分别求出相应的概率,由此能求出X的分布列.
(2)离散型随机变量X的取值可能为:0,1,2,3,分别求出相应的概率,由此能求出X的分布列.
解答:
解:(1)设黑球的个数为x,则白球的个数为10-x.
记两个都是黑球得的事件为A,则至少有一个白球的事件与事件A为对立事件
所以p(A)=1-
=
=
,解得x=5,
所以白球的个数为5.(6分)
(2)离散型随机变量X的取值可能为:0,1,2,3,
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
所以X的分布列为
(12分).
记两个都是黑球得的事件为A,则至少有一个白球的事件与事件A为对立事件
所以p(A)=1-
| 7 |
| 9 |
| ||
|
| 2 |
| 9 |
所以白球的个数为5.(6分)
(2)离散型随机变量X的取值可能为:0,1,2,3,
P(X=0)=
| ||||
|
| 1 |
| 12 |
P(X=1)=
| ||||
|
| 5 |
| 12 |
P(X=2)=
| ||||
|
| 5 |
| 12 |
P(X=3)=
| ||||
|
| 1 |
| 12 |
所以X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
点评:本题考查白球个数的求法,考查X的分布列的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
曲线y=
x3-2在点(1,-
) 处切线的斜率为( )
| 1 |
| 3 |
| 5 |
| 3 |
A、
| ||
| B、1 | ||
| C、-1 | ||
D、-
|
已知2a+1<0,关于x的不等式x2-4ax-5a2>0的解集是( )
| A、{x|x>5a或x<-a} |
| B、{x|-a<x<5a} |
| C、{x|x<5a或x>-a} |
| D、{x|5a<x<-a} |
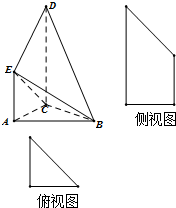 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.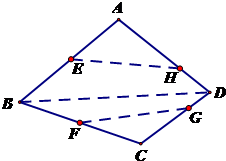 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是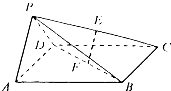 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.