题目内容
已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为多少?
考点:圆的切线方程
专题:直线与圆
分析:求出圆的圆心与半径,利用四边形的最小值求出PC的最小值,利用点到直线的距离求解即可.
解答:
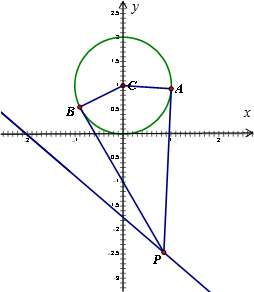 解:圆C:x2+y2-2y=0⇒x2+(y-1)2=1,圆心C(0,1),半径为1;…(2分)
解:圆C:x2+y2-2y=0⇒x2+(y-1)2=1,圆心C(0,1),半径为1;…(2分)
如图,∵PA=PB,CB⊥PB,CA⊥PA,
∴SPACB=2•
•PA•CA=PA…(4分).
∵SPACD≥2,∴PA≥2…(6分).
∵PC2=PA2+CA2=PA2+1,∴PC2≥5
即点C到直线的距离为
…(8分)
所以d=
=
,…(11分)
解得:k=±2(负舍)…(12分)
所以k=2…(13分)
 解:圆C:x2+y2-2y=0⇒x2+(y-1)2=1,圆心C(0,1),半径为1;…(2分)
解:圆C:x2+y2-2y=0⇒x2+(y-1)2=1,圆心C(0,1),半径为1;…(2分)如图,∵PA=PB,CB⊥PB,CA⊥PA,
∴SPACB=2•
| 1 |
| 2 |
∵SPACD≥2,∴PA≥2…(6分).
∵PC2=PA2+CA2=PA2+1,∴PC2≥5
即点C到直线的距离为
| 5 |
所以d=
| |1+4| | ||
|
| 5 |
解得:k=±2(负舍)…(12分)
所以k=2…(13分)
点评:本题考查直线与圆的位置关系,点到直线的距离公式的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
若复数z满足z=1-2i,则z的虚部为( )
| A、-2i | B、2i | C、-2 | D、2 |
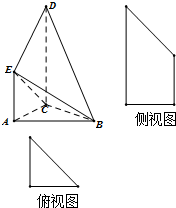 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.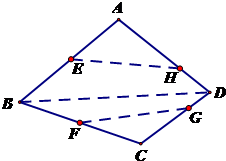 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是