题目内容
已知函数f(x)=ax2-(a+2)x+lnx(a>0).
(1)若a=1,求函数f(x)的极值;
(2)讨论函数f(x)的单调性.
(1)若a=1,求函数f(x)的极值;
(2)讨论函数f(x)的单调性.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)a=1时,f(x)=x2-3x+lnx,通过求导得到函数的极值点,从而求出极值.
(2)通过求解函数的导函数,通过:当0<a<2,a=2,a>2,分别通过函数的导数列表,然后求函数f(x)的单调区间.
(2)通过求解函数的导函数,通过:当0<a<2,a=2,a>2,分别通过函数的导数列表,然后求函数f(x)的单调区间.
解答:
解:(1)a=1时,f(x)=x2-3x+lnx,
∴f′(x)=2x-3+
,
f′(x)>0时,解得:x>1,x<
f(x)<0时,解得:
<x<1,
∴函数f(x)在(0,
),(1,+∞)递增,在(
,1)递减,
∴x=
是极大值点,x=1是极小值点,
∴f(
)=-
-ln2,f(1)=-2.
(2)f′(x)=2ax-(a+2)+
=
,
①当0<a<2时,
当x∈(0,
)时,f′(x)>0,函数是增函数;
当x∈(
,
)时,f′(x)<0,函数是减函数;
当x∈(
,+∞)时,f′(x)>0,函数是增函数.
②当a=2时,f′(x)=
,对一切x∈(0,+∞)恒成立,
当且仅当x=1时f′(x)=0,函数是单调增函数,单调增区间(0,+∞)
③当a>2时,
综上:当x∈(0,
)时,f′(x)>0,函数是增函数;
当x∈(
,
)时,f′(x)<0,函数是减函数;
当x∈(
,+∞)时,f′(x)>0,函数是增函数.
当0<a<2时,函数f(x)的单调增区间(0,
)和(
,+∞),单调减区间是(
,
).
当a=2时,函数的单调增区间(0,+∞)
当a>2时,函数f(x)的单调增区间(0,
)和(
,+∞),单调减区间是(
,
).
∴f′(x)=2x-3+
| 1 |
| x |
f′(x)>0时,解得:x>1,x<
| 1 |
| 2 |
f(x)<0时,解得:
| 1 |
| 2 |
∴函数f(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
| 5 |
| 4 |
(2)f′(x)=2ax-(a+2)+
| 1 |
| x |
| (ax-1)(2x-1) |
| x |
①当0<a<2时,
当x∈(0,
| 1 |
| 2 |
当x∈(
| 1 |
| 2 |
| 1 |
| a |
当x∈(
| 1 |
| a |
②当a=2时,f′(x)=
| (2x-1)2 |
| x |
当且仅当x=1时f′(x)=0,函数是单调增函数,单调增区间(0,+∞)
③当a>2时,
综上:当x∈(0,
| 1 |
| a |
当x∈(
| 1 |
| a |
| 1 |
| 2 |
当x∈(
| 1 |
| 2 |
当0<a<2时,函数f(x)的单调增区间(0,
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
当a=2时,函数的单调增区间(0,+∞)
当a>2时,函数f(x)的单调增区间(0,
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
点评:本题考查函数的导数的综合应用,函数的单调性函数的极值,考查分类讨论以及计算能力.

练习册系列答案
相关题目
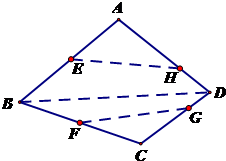 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是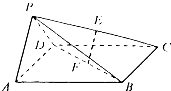 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.