题目内容
函数y=2x+sinx的单调增区间是（ ）
| A、（-∞，+∞） | ||||
| B、（0，+∞） | ||||
C、（2kπ-
| ||||
| D、以上答案均不正确 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求函数的定义域，在求函数的导函数y′，利用余弦函数的有界性发现y′＞0，故此函数在定义域上为增函数
解答：
解：y=2x+sinx的定义域为R，
∵y′=2+cosx，且cosx∈[-1，1]
∴y′＞0
∴函数y=2x+sinx的单调递增区间是（-∞，+∞）
故选：A．
∵y′=2+cosx，且cosx∈[-1，1]
∴y′＞0
∴函数y=2x+sinx的单调递增区间是（-∞，+∞）
故选：A．
点评：本题考察了导数在函数单调性中的应用，三角函数的有界性等基础知识．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
下列各式中，值为
的是（ ）
| 1 |
| 2 |
| A、sin15°•cos15° | ||||
B、2cos2
| ||||
C、
| ||||
D、
|
曲线y=
x3-2在点（1，-
） 处切线的斜率为（ ）
| 1 |
| 3 |
| 5 |
| 3 |
A、
| ||
| B、1 | ||
| C、-1 | ||
D、-
|
若复数z满足z=1-2i，则z的虚部为（ ）
| A、-2i | B、2i | C、-2 | D、2 |
现有60件产品，编号从1到60，若用系统抽样方法从中抽取6件检验，则所抽到的个体编号可能是（ ）
| A、5，10，15，20，25，30 |
| B、2，14，26，28，42，56 |
| C、5，8，31，36，48，54 |
| D、3，13，23，33，43，53 |
若函数f（x）的零点与g（x）=lnx+2x-8的零点之差的绝对值不超过0.5，则f（x）可以是（ ）
| A、f（x）=3x-6 | ||
| B、f（x）=（x-4）2 | ||
| C、f（x）=ex-1-1 | ||
D、f（x）=ln（x-
|
已知2a+1＜0，关于x的不等式x2-4ax-5a2＞0的解集是（ ）
| A、{x|x＞5a或x＜-a} |
| B、{x|-a＜x＜5a} |
| C、{x|x＜5a或x＞-a} |
| D、{x|5a＜x＜-a} |
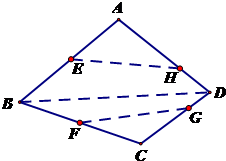如图，在空间四边形ABCD中，E，F分别是AB和CB上的点，G，F分别是