题目内容
某种灯泡使用寿命在1000小时以上的概率为0.2,某同学家一共用了这种灯泡4只.设这4只灯泡在使用1000小时后,坏了的灯泡数为随机变量X.
(1)求随机变量X的概率分布;
(2)求随机变量X的数学期望和方差.
(1)求随机变量X的概率分布;
(2)求随机变量X的数学期望和方差.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)随机变量X的取值为0,1,2,3,4,由题意知P(X=k)=
•0.8k•0.24-k,其中k=0,1,2,3,4.由此能求出随机变量X的分布列.
(2)由(1)能求出随机时变量X的数学期望和随机变量X的方差.
| C | k 4 |
(2)由(1)能求出随机时变量X的数学期望和随机变量X的方差.
解答:
解:(1)随机变量X的取值为0,1,2,3,4,
在使用1000小时后,灯泡坏了的概率p=1-0.2=0.8,
P(X=k)=
•0.8k•0.24-k,其中k=0,1,2,3,4.
∴随机变量X的分布列为:
(2)由(1)知:
随机时变量X的数学期望为:
E(X)=0.0256+2×0.1536+3×0.4096+4×0.4096=3.2.
随机变量X的方差为:
V(x)=(0-3.2)2×0.0016+(1-3.2)2×0.0256+(2-3.2)2×0.1536
+(3-3.2)2×0.4096+(4-3.2)2×0.4096=0.64.
在使用1000小时后,灯泡坏了的概率p=1-0.2=0.8,
P(X=k)=
| C | k 4 |
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.0016 | 0.0256 | 0.1536 | 0.4096 | 0.4096 |
随机时变量X的数学期望为:
E(X)=0.0256+2×0.1536+3×0.4096+4×0.4096=3.2.
随机变量X的方差为:
V(x)=(0-3.2)2×0.0016+(1-3.2)2×0.0256+(2-3.2)2×0.1536
+(3-3.2)2×0.4096+(4-3.2)2×0.4096=0.64.
点评:本题考查离散型随机变量的分布列的求法,考查随机变量的数学期望和方差的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
若函数f(x)的零点与g(x)=lnx+2x-8的零点之差的绝对值不超过0.5,则f(x)可以是( )
| A、f(x)=3x-6 | ||
| B、f(x)=(x-4)2 | ||
| C、f(x)=ex-1-1 | ||
D、f(x)=ln(x-
|
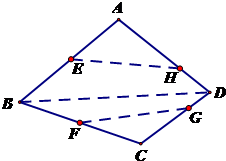 如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是
如图,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,F分别是