题目内容
已知抛物线方程为y2=2px(p>0),经过焦点且倾斜角为135°的直线,被抛物线所截得的弦长为8.
(1)试求抛物线方程;
(2)若该抛物线的焦点为F,准线与x轴的交点为M,N为抛物线上的一点,且满足NF=
MN,求∠NMF的大小.
(1)试求抛物线方程;
(2)若该抛物线的焦点为F,准线与x轴的交点为M,N为抛物线上的一点,且满足NF=
| ||
| 2 |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)依题意,设抛物线方程为y2=2px,可求得过焦点且倾斜角为135°的直线方程为y=-x+
p,利用抛物线的定义结合题意可求得p,从而可求得抛物线方程,
(2)根据抛物线的定义,N作准线的垂线,垂足为G,NG=d=NF,构成直角三角形,利用角的互余求解运算.
| 1 |
| 2 |
(2)根据抛物线的定义,N作准线的垂线,垂足为G,NG=d=NF,构成直角三角形,利用角的互余求解运算.
解答:
解:(1)依题意,设抛物线方程为y2=2px,则直线方程为y=-x+
p.设直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B分别作准线的垂线,垂足分别为C、D.
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|
=x1+
+x2+
即x1+
+x2+
=8.①
又A(x1,y1)、B(x2,y2)是抛物线和直线的交点,
由
消去y,得x2-3px+
=0,
∵△=9p2-4×
=8p2>0.
∴x1+x2=3p.
将其代入①得p=2,
∴所求抛物线方程为y2=4x.
(2)根据抛物线的定义可知:N到准线的距离=d=|NF|,
∵NF=
MN,
∴N作准线的垂线,垂足为G,根据定义可知:sin∠GMN=
=
=
,
即∠NMG=
∵∠NMF+∠GMN=
,
∴∠NMF=
故∠NMF的大小为:
,
| 1 |
| 2 |
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|
=x1+
| p |
| 2 |
| p |
| 2 |
即x1+
| p |
| 2 |
| p |
| 2 |
又A(x1,y1)、B(x2,y2)是抛物线和直线的交点,
由
|
| p2 |
| 4 |
∵△=9p2-4×
| p2 |
| 4 |
∴x1+x2=3p.
将其代入①得p=2,
∴所求抛物线方程为y2=4x.
(2)根据抛物线的定义可知:N到准线的距离=d=|NF|,
∵NF=
| ||
| 2 |
∴N作准线的垂线,垂足为G,根据定义可知:sin∠GMN=
| d |
| MN |
| NF |
| MN |
| ||
| 2 |
即∠NMG=
| π |
| 3 |
∵∠NMF+∠GMN=
| π |
| 2 |
∴∠NMF=
| π |
| 6 |
故∠NMF的大小为:
| π |
| 6 |
点评:本题考察了抛物线的定义,几何性质,充分利用了到焦点的距离和到准线的距离相等这个条件,在计算中的作用.

练习册系列答案
相关题目
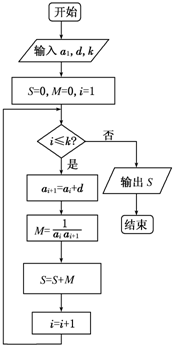 已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=
已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |
函数f(x)=-sinx+1的图象大致为( )
A、 |
B、 |
C、 |
D、 |