题目内容
12.设Tn为数列{an}的前n项之积,即Tn=a1a2a3…an-1an,若a1=2,$\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1(n∈{N^*},n≥2)$,当Tn=11时,n的值为10.分析 由题意可得数列{$\frac{1}{{a}_{n}-1}$}是以$\frac{1}{{a}_{1}-1}$为首项,以1为公差的等差数列,写出通项公式,求出an,再写出Tn,令Tn=11求得n的值.
解答 解:由a1=2,$\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1(n∈{N^*},n≥2)$,
可得数列{$\frac{1}{{a}_{n}-1}$}是以$\frac{1}{{a}_{1}-1}$为首项,以1为公差的等差数列,
∴$\frac{1}{{a}_{n}-1}$=1+(n-1)•1=n,
∴an=1+$\frac{1}{n}$=$\frac{n+1}{n}$,
∴Tn=a1a2a3…an-1an=2•$\frac{3}{2}$•$\frac{4}{3}$…$\frac{n+1}{n}$=n+1,
由Tn=n+1=11,得n=10.
故答案为:10.
点评 本题考查了数列递推式,以及累积法求数列通项公式的应用问题,是中档题.

练习册系列答案
相关题目
17.已知$x∈({0,\frac{π}{2}})$,p:sinx<x,q:sinx<x2,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.函数f(x)=lg(|x|-1)的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
1.一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为( )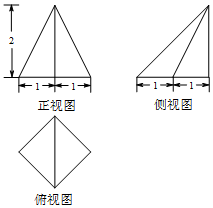

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |