题目内容
16.某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角A、B、C所对的边分别是a,b,c)得出如下一些结论:(1)若△ABC是钝角三角形,则tanA+tanB+tanC>0;
(2)若△ABC是锐角三角形,则cosA+cosB>sinA+sinB;
(3)在三角形△ABC中,若A<B,则cos(sinA)<cos(tanB)
(4)在△ABC中,若$sinB=\frac{2}{5},tanC=\frac{3}{4}$,则A>C>B
其中错误命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 (1)利用正切的和角公式变形形式tanA+tanB=tan(A+B)(1-tanAtanB)化简整理.
(2)根据三角形是锐角三角形,得到A+B>90°,变形为B>90°-A,根据三角函数在第一象限的单调性,得到cosB<sinA,sinB>cosA,即可得解;
(3)当B=$\frac{π}{2}$时,不等式不成立;
(4)根据sinB=$\frac{2}{5}$,讨论B为锐角或钝角,利用特殊角的三角函数值及正弦函数的增减性确定出B的范围;根据tan C=$\frac{3}{4}$可知C为锐角,根据正切函数的增减性和特殊角的三角函数值得到角C的范围,再根据内角和定理得到A的范围即可比较大小.
解答 解:(1)∵tanA+tanB=tan(A+B)(1-tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=tanAtanBtanC,
∴△ABC是钝角三角形,可得:tanAtanBtanC<0,故错误;
(2)∵△ABC为锐角三角形,
∴A+B>90°,B>90°-A,
∴cosB<sinA,sinB>cosA,
∴cosB-sinA<0,sinB-cosA>0,
∴cosB-sinA<sinB-cosA,可得cosA+cosB<sinA+sinB,故错误;
(3)当B=$\frac{π}{2}$时,tanB不存在,故错误;
(4)由tanC=$\frac{3}{4}$得到0<C<90°,且tan30°=$\frac{\sqrt{3}}{3}$<$\frac{3}{4}$<1=tan45°,
因为正切函数在(0,90°)为增函数,所以得到30°<C<45°;
由sinB=$\frac{2}{5}$可得到0<B<90°或90°<B<180°,
在0<B<90°时,sin30°=$\frac{1}{2}$>$\frac{2}{5}$,因为正弦函数在(0,90°)为增函数,得到0<B<30°;
在90°<B<180°时,sin150°=$\frac{1}{2}$>$\frac{2}{5}$,但是正弦函数在90°<B<180°为减函数,得到B>150°,则B+C>180°,
矛盾,不成立.
所以0<B<30°.由B和C的取值得到A为钝角,
所以A>C>B,故正确;
故选:D.
点评 本题考查两角和的正切公式以及三角函数的符号,训练运用公式熟练变形的能力,考查学生会根据三角函数值的范围及三角函数的增减性和特殊角的三角函数值来比较角度的大小,考查了转化思想,属于中档题.

 高中必刷题系列答案
高中必刷题系列答案| A. | 1365石 | B. | 336石 | C. | 168石 | D. | 134石 |
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
| A. | (2,4) | B. | (1,3) | C. | (1,2) | D. | (2,3) |
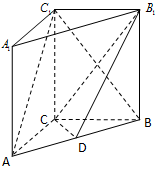 如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中侧棱垂直于底面,AC⊥BC,点D是AB的中点.