计算下列式子:+,,(3)$\frac{3+i}{2+i}$．题目和参考答案——青夏教育精英家教网——

题目内容

13．计算下列式子：
（1）（-2-4i）-（-2+i）+（1+7i）；
（2）（1+i）（2+i）（3+i）；
（3）$\frac{3+i}{2+i}$．

分析直接由复数代数形式的加减运算求解（1）；由复数代数形式的乘除运算化简（2）、（3）．

解答解：（1）（-2-4i）-（-2+i）+（1+7i）=-2+2+1-4i-i+7i=1+2i；
（2）（1+i）（2+i）（3+i）═（2+3i+i²）（3+i）=（1+3i）（3+i）=3+10i+3i²=10i；
（3）$\frac{3+i}{2+i}$=$\frac{（3+i）（2-i）}{（2+i）（2-i）}=\frac{7-i}{5}=\frac{7}{5}-\frac{1}{5}i$．

点评本题考查了复数代数形式的乘除运算，是基础题．

练习册系列答案

毕业会考阶梯模拟卷系列答案

小学升学多伦夯基总复习系列答案

同步练习目标与测试系列答案

复习计划风向标暑系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

全品中考试卷系列答案

全效系列丛书赢在期末系列答案

新天地期末系列答案

相关题目

3．总体由编号为01，02，03，…，49，50的50个个体组成，利用随机数表（以下选取了随机数表中的第1行和第2行）选取5个个体，选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取，则选出来的第4个个体的编号为（　　）

78 16 65 72 08 02 63 14 07 02 43 69 69 38 74

32 04 94 23 49 55 80 20 36 35 48 69 97 28 01

4．若y=sinxsin（x+$\frac{π}{3}$+φ）是一个奇函数，则φ可能的取值是（　　）

$\frac{2π}{3}$

1．在数列{a_n}中，a₁=1，并且对于任意n∈N^*，都有${a_{n+1}}=\frac{a_n}{{2{a_n}+1}}$．
（1）证明数列$\left\{{\frac{1}{a_n}}\right\}$为等差数列，并求{a_n}的通项公式；
（2）设数列b_n=a_n．a_n+1，求数列{b_n}的前n项和为T_n．

8．若函数f（x）=sinx+3|sinx|在x∈[0，2π]与直线y=2a有两个交点，则a的取值范围为（　　）

5．已知函数f（x）=2e^x-m-x，其中m为实数．
（1）当m=ln2时，求函数f（x）的单调区间；
（2）若m≤1，对任意x∈R，记f（x）的最小值为g（m），求g（m）的最小值．

12．设T_n为数列{a_n}的前n项之积，即T_n=a₁a₂a₃…a_n-1a_n，若a₁=2，$\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1（n∈{N^*}，n≥2）$，当T_n=11时，n的值为10．

9．定义在R上的可导函数f（x），其导函数记为f'（x），满足f（x）+f（2-x）=（x-1）²，且当x≤1时，恒有f'（x）+2＜x．若$f（m）-f（{1-m}）≥\frac{3}{2}-3m$，则实数m的取值范围是（　　）

$（{-\frac{1}{3}，1}]$

$（{-∞，\frac{1}{2}}]$

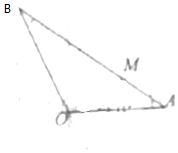如图，在△AOB中，∠AOB=$\frac{3π}{4}$，OA=6，M为边AB上一点，M到边OA，OB的距离分别为2，2$\sqrt{2}$，则AB的长为6$\sqrt{5}$．