题目内容
解方程:log2(2-x-1)•log
(2-x+1-2)=-2.
| 1 |
| 2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:log2(2-x-1)•log
(2-x+1-2)=-2.化为log2(2-x-1)•(-1-log2(2-x-1))=-2,因式分解为(log2(2-x-1))2+log2(2-x-1)-2=0,再利用对数的运算性质即可得出.
| 1 |
| 2 |
解答:
解:∵log2(2-x-1)•log
(2-x+1-2)=-2.
∴log2(2-x-1)•(-1-log2(2-x-1))=-2,
化为(log2(2-x-1))2+log2(2-x-1)-2=0,
∴(log2(2-x-1)+2)(log2(2-x-1)-1)=0,
∴log2(2-x-1)+2=0,log2(2-x-1)-1=0.
∴2-x-1=2-2,2-x-1=2,
解得x=-log2
,x=-log23.
经过检验满足条件.
| 1 |
| 2 |
∴log2(2-x-1)•(-1-log2(2-x-1))=-2,
化为(log2(2-x-1))2+log2(2-x-1)-2=0,
∴(log2(2-x-1)+2)(log2(2-x-1)-1)=0,
∴log2(2-x-1)+2=0,log2(2-x-1)-1=0.
∴2-x-1=2-2,2-x-1=2,
解得x=-log2
| 5 |
| 4 |
经过检验满足条件.
点评:本题考查了对数型一元二次方程的解法、对数的运算法则,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
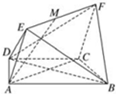 如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=
如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=