题目内容
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,一直曲线C:ρsin2θ=2acosθ(a>0),过点P(-2,-4)的直线l的参数方程为
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
|
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)首先,对于曲线C:根据极坐标与直角坐标变换公式
,方程ρsin2θ=2acosθ(a>0),两边同乘以ρ,化成直角坐标方程,对于直线l:消去参数t即可得到普通方程;
(2)首先,联立方程组
,消去y整理,然后,设点M,N分别对应参数t1,t2,从而,得到|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|,然胡,结合一元二次方程根与系数的关系,建立含有a的关系式,求解a的取值.
|
(2)首先,联立方程组
|
解答:
解:(1)∵
,
方程ρsin2θ=2acosθ(a>0),两边同乘以ρ,
∴曲线C的直角坐标方程为y2=2ax(a>0);
直线l的普通方程为x-y-2=0.
(2)联立方程组
,
消去y并整理,得
t2-2(4+a)
t+8(4+a)=0 (*)
△=8a(4+a)>0.
设点M,N分别对应参数t1,t2,恰为上述方程的根.
则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.
由题设得(t1-t2)2=|t1t2|,
即(t1+t2)2-4t1t2=|t1t2|.
由(*)得t1+t2=2(4+a)
,t1t2=8(4+a)>0,则有
(4+a)2-5(4+a)=0,得a=1,或a=-4.
∵a>0,
∴a=1.
|
方程ρsin2θ=2acosθ(a>0),两边同乘以ρ,
∴曲线C的直角坐标方程为y2=2ax(a>0);
直线l的普通方程为x-y-2=0.
(2)联立方程组
|
消去y并整理,得
t2-2(4+a)
| 2 |
△=8a(4+a)>0.
设点M,N分别对应参数t1,t2,恰为上述方程的根.
则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.
由题设得(t1-t2)2=|t1t2|,
即(t1+t2)2-4t1t2=|t1t2|.
由(*)得t1+t2=2(4+a)
| 2 |
(4+a)2-5(4+a)=0,得a=1,或a=-4.
∵a>0,
∴a=1.
点评:本题重点考查了极坐标方程和直角坐标方程的互化,参数方程和普通方程的互化,直线与曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目
若方程
+
=1表示准线平行于x轴的椭圆,则m的范围是( )
| x2 |
| m2 |
| y2 |
| (1-m)2 |
A、m>
| ||
B、m<
| ||
C、m>
| ||
D、m<
|
长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于( )
| A、30° | B、45° |
| C、60° | D、90° |
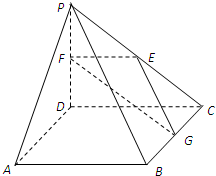 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.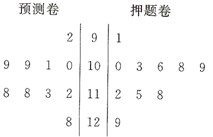 安徽某所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟考试,检测成绩的茎叶图如图所示.
安徽某所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟考试,检测成绩的茎叶图如图所示. 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题: