题目内容
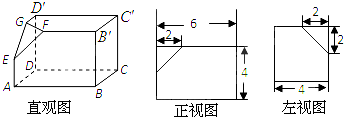
长方体ABCD-A1B1C1D1中，异面直线AB，A1D1所成的角等于（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：由长方体的特点可得AB与AD所成的角即为异面直线AB，A1D1所成的角，由矩形的性质可求．
解答：
解：∵长方体ABCD-A1B1C1D1中，DA∥A1D1，
∴AB与AD所成的角即为异面直线AB，A1D1所成的角，
在矩形ABCD中易得AB与AD所成的角为90°，
故异面直线AB，A1D1所成的角等于90°
故选：D
∴AB与AD所成的角即为异面直线AB，A1D1所成的角，
在矩形ABCD中易得AB与AD所成的角为90°，
故异面直线AB，A1D1所成的角等于90°
故选：D
点评：本题考查异面直线所成的角，属基础题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
α：x=1，β：x2=1，则α是β的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
设函数f（x）=
，若f-1（4）=a，则实数a=（ ）
|
| A、1或2 | B、-1或2 |
| C、1或-2 | D、-1或2 |
