题目内容
设等比数列{an}的前n项和为Sn(n∈N*).若S3,S9,S6成等差数列,则
的值是 .
| a8 |
| a2+a5 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:设等比数列{an}的公比为q、首项是a1,根据公比q与1的关系进行分类,由等比数列的前n项和公式化简求值,再由等比数列的通项公式化简所求的式子即可.
解答:
解:设等比数列{an}的公比为q、首项是a1,
当q=1时,有S3=3a1、S9=9a1、S6=a1,不满足S3,S9,S6成等差数列;
当q≠1时,因为S3,S9,S6成等差数列,
所以2×
=
+
,
化简得2q6-q3-1=0,解得q3=-
或q3=1(舍去),
则
=
=
=
,
故答案为:
.
当q=1时,有S3=3a1、S9=9a1、S6=a1,不满足S3,S9,S6成等差数列;
当q≠1时,因为S3,S9,S6成等差数列,
所以2×
| a1(1-q9) |
| 1-q |
| a1(1-q3) |
| 1-q |
| a1(1-q6) |
| 1-q |
化简得2q6-q3-1=0,解得q3=-
| 1 |
| 2 |
则
| a8 |
| a2+a5 |
| a1q7 |
| a1q+a1q4 |
| q6 |
| 1+q3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查等比数列的前n项和公式、通项公式,分类讨论思想,使用等比数列的前n项和公式时需要对公比与1的关系进行讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
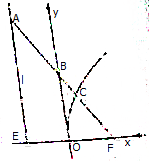 如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若
如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
