题目内容
已知函数f(x)=x-a-alnx(a∈R).
(Ⅰ)当函数y=f(x)有两个零点时,求实数a的取值范围;
(Ⅱ)当函数y=f(x)有两个零点x1,x2∈[
,
]且x1<x2时,证明:
①若x2-x1≤1,则有
<a<
;
②
随着a的增大而增大;
③x1x2>1;
(Ⅲ)证明:
>ln(n+1),(n∈N*).
(Ⅰ)当函数y=f(x)有两个零点时,求实数a的取值范围;
(Ⅱ)当函数y=f(x)有两个零点x1,x2∈[
| 1 |
| 2 |
| 5 |
| 2 |
①若x2-x1≤1,则有
| 3 |
| ln2+ln9 |
| 1 |
| 2-ln4 |
②
| x2-x1 |
| x1x2 |
③x1x2>1;
(Ⅲ)证明:
| ||
| k=1 |
| k |
| 1+lnk |
考点:不等式的证明,利用导数研究函数的极值,不等式的综合
专题:计算题,证明题,函数的性质及应用
分析:(Ⅰ)由题意得,x-a-alnx=0,从而可得a=
,x>0,令g(x)=
并求导g′(x)=
,从而得出单调区间,作图解答;
(Ⅱ)①由(Ⅰ)得a=
,再由x2-x1≤1及函数y=
单调性得f(
)<f(
),从而解得,
②由(Ⅰ)得,a=
=
,
=
-
=
-
,令φ(x)=
,从而可得φ(x)=
在[
,
]上单调递增,从而可得;
③a=
,lna=lnx-ln(1+lnx),令u=1+lnx,
,(t>1),则u2+u1=
lnt,(t>1);从而可得x1x2>1;
(Ⅲ)ln(n+1)=
(ln(k+1)-lnk)=
ln(
);故
>ln(n+1),(n∈N*)可化为
>
ln(
),从而转化为
>ln
;从而证明.
| x |
| 1+lnx |
| x |
| 1+lnx |
| lnx |
| (1+lnx)2 |
(Ⅱ)①由(Ⅰ)得a=
| x |
| 1+lnx |
| x |
| 1+lnx |
| 3 |
| 2 |
| 1 |
| 2 |
②由(Ⅰ)得,a=
| x1 |
| 1+lnx1 |
| x2 |
| 1+lnx2 |
| x2-x1 |
| x1x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| lnx2 |
| x2 |
| lnx1 |
| x1 |
| x |
| lnx |
| x |
| lnx |
| 1 |
| 2 |
| 5 |
| 2 |
③a=
| x |
| 1+lnx |
|
| t-1 |
| t+1 |
(Ⅲ)ln(n+1)=
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| k+1 |
| k |
| ||
| k=1 |
| k |
| 1+lnk |
| ||
| k=1 |
| k |
| 1+lnk |
| n |
 |
| k=1 |
| k+1 |
| k |
| k |
| 1+lnk |
| k+1 |
| k |
解答:
解:(Ⅰ)∵f(x)=x-a-alnx(a∈R).
∴x-a-alnx=0,(a∈R).
又∵当1+lnx=0,即x=
时,上式不成立,
∴a=
,x>0,
令g(x)=
,则g′(x)=
,
当g′(x)=
>0时,x>1,
当g′(x)=
<0时,0<x<
,
<x<1
当g′(x)=
=0时,x=1,
g(x)在(0,
),(
,1)单调递减,在(1,+∞)单调递增,
其图象如下,

当x>
时,g(x)≥g(1)=
=1,
∴g(x)与y=a交点为2个交点时,
∴a>1,
∴函数y=f(x)有两个零点时,a>1,
(Ⅱ)①令f(x)=0,得a=
,
由x2-x1≤1,及函数y=
单调性,
得f(
)<f(
),即得
<a<
,
<
,
故得证
<a<
;
②由(Ⅰ)得,f(x)有两个零点时,a>1,
∵f(x1)-f(x2)=0,
∴a=
=
,
=
-
=
-
,
令φ(x)=
,得
=φ(x2)-φ(x1),
设ξ,η∈(1,+∞),且ξ<η,
ξ=g(ξ1)=g(ξ2),其中
<ξ1<1<ξ2≤
,
,η=g(η1)=g(η2),其中
<η1<1<η2≤
,
由函数g(x)的单调性可知,g(ξ1)<g(η1),ξ1<η1,
同理ξ2>η2,
故
≤ξ1<η1<1<η2<ξ2≤
,∵φ(x)=
在[
,
]上单调递增,∴
φ(ξ1)<φ(η1),φ(ξ2)>φ(η2),
由②得:φ(ξ2)-φ(η2)-[φ(ξ1)-φ(η1)]>0,
∴
随着a的增大而增大;
③a=
,
lna=lnx-ln(1+lnx),
令u=1+lnx,
lnx=u-1,
则lnx2-ln(1+lnx2)=lnx1-ln(1+lnx1)=lnx2-lnx1=ln(1+lnx2)-ln(1+lnx1),
u2-u1=lnu2-lnu1,
,(t>1)
则u2+u1=
lnt,(t>1);
令h(x)=
lnx,x∈(1,+∞);
则h′(x)=
;
令m(x)=-2lnx+x-
,从而可得m′(x)=(
)2,
故m(x)=-2lnx+x-
是(1,+∞)的增函数,
故h(x)是(1,+∞)的增函数,
且
=2;
故u2+u1>2;
则1+lnx1+1+lnx2>2;
故x1x2>1;
(Ⅲ)证明:ln(n+1)=
(ln(k+1)-lnk)
=
ln(
);
故
>ln(n+1),(n∈N*)可化为
>
ln(
),
即证
>ln
;
而
>
>
>ln
,
故
>ln(n+1),(n∈N*).
∴x-a-alnx=0,(a∈R).
又∵当1+lnx=0,即x=
| 1 |
| e |
∴a=
| x |
| 1+lnx |
令g(x)=
| x |
| 1+lnx |
| lnx |
| (1+lnx)2 |
当g′(x)=
| lnx |
| (1+lnx)2 |
当g′(x)=
| lnx |
| (1+lnx)2 |
| 1 |
| e |
| 1 |
| e |
当g′(x)=
| lnx |
| (1+lnx)2 |
g(x)在(0,
| 1 |
| e |
| 1 |
| e |
其图象如下,

当x>
| 1 |
| e |
| 1 |
| 1+ln1 |
∴g(x)与y=a交点为2个交点时,
∴a>1,
∴函数y=f(x)有两个零点时,a>1,
(Ⅱ)①令f(x)=0,得a=
| x |
| 1+lnx |
由x2-x1≤1,及函数y=
| x |
| 1+lnx |
得f(
| 3 |
| 2 |
| 1 |
| 2 |
| 3 | ||
2+ln
|
| 1 |
| 2-ln4 |
| 3 |
| ln2+ln9 |
| 3 | ||
2+ln
|
故得证
| 3 |
| ln2+ln9 |
| 1 |
| 2-ln4 |
②由(Ⅰ)得,f(x)有两个零点时,a>1,
∵f(x1)-f(x2)=0,
∴a=
| x1 |
| 1+lnx1 |
| x2 |
| 1+lnx2 |
| x2-x1 |
| x1x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| lnx2 |
| x2 |
| lnx1 |
| x1 |
令φ(x)=
| x |
| lnx |
| x2-x1 |
| x1x2 |
设ξ,η∈(1,+∞),且ξ<η,
ξ=g(ξ1)=g(ξ2),其中
| 1 |
| 2 |
| 5 |
| 2 |
,η=g(η1)=g(η2),其中
| 1 |
| 2 |
| 5 |
| 2 |
由函数g(x)的单调性可知,g(ξ1)<g(η1),ξ1<η1,
同理ξ2>η2,
故
| 1 |
| 2 |
| 5 |
| 2 |
| x |
| lnx |
| 1 |
| 2 |
| 5 |
| 2 |
φ(ξ1)<φ(η1),φ(ξ2)>φ(η2),
由②得:φ(ξ2)-φ(η2)-[φ(ξ1)-φ(η1)]>0,
∴
| x2-x1 |
| x1x2 |
③a=
| x |
| 1+lnx |
lna=lnx-ln(1+lnx),
令u=1+lnx,
lnx=u-1,
则lnx2-ln(1+lnx2)=lnx1-ln(1+lnx1)=lnx2-lnx1=ln(1+lnx2)-ln(1+lnx1),
u2-u1=lnu2-lnu1,
|
则u2+u1=
| t-1 |
| t+1 |
令h(x)=
| (x+1) |
| x-1 |
则h′(x)=
-2lnx+x-
| ||
| (x-1)2 |
令m(x)=-2lnx+x-
| 1 |
| x |
| x-1 |
| x |
故m(x)=-2lnx+x-
| 1 |
| x |
故h(x)是(1,+∞)的增函数,
且
| limh(x) |
| x→1 |
故u2+u1>2;
则1+lnx1+1+lnx2>2;
故x1x2>1;
(Ⅲ)证明:ln(n+1)=
| n |
 |
| k=1 |
=
| n |
 |
| k=1 |
| k+1 |
| k |
故
| ||
| k=1 |
| k |
| 1+lnk |
| ||
| k=1 |
| k |
| 1+lnk |
| n |
 |
| k=1 |
| k+1 |
| k |
即证
| k |
| 1+lnk |
| k+1 |
| k |
而
| k |
| 1+lnk |
| 1+lnk |
| k |
| 1 |
| k |
| k+1 |
| k |
故
| ||
| k=1 |
| k |
| 1+lnk |
点评:本题考查了导数的综合应用,不等式的证明及放缩法的应用,属于中档题.

练习册系列答案
相关题目
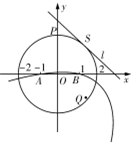 如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.
如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.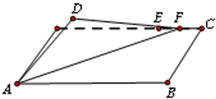 如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为
如图,在长方形ABCD中,AB=4,BC=1,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为