题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,其左焦点为F(-
,0).
(1)求椭圆C的方程;
(2)已知点D(1,0)直线:y=kx+m(k≠0)与椭圆C交于A,B两点,设线段AB的中点为M若DM⊥AB,试求k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)已知点D(1,0)直线:y=kx+m(k≠0)与椭圆C交于A,B两点,设线段AB的中点为M若DM⊥AB,试求k的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得
,由此能求出椭圆方程.
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),由
,得(4k2+1)x2+8kmx+4(m2-1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出k的取值范围.
|
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),由
|
解答:
解:(1)由题意得
,
解得a=2,b=1,
∴椭圆方程为
+y2=1.
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),
由
,得(4k2+1)x2+8kmx+4(m2-1)=0,
∵直线:y=kx+m(k≠0)与椭圆C交于A,B两点,
∴△=64k2-16(4k2+1)(m2-1)>0,
解得4k2+1>m2,①
x1+x2=-
,
∴x0=-
,y0=
,
由题意知DM垂直平分AB,∴DM的方程为x=-ky+1,
将点M的坐标代入,得m=-
,②
由①②,得4k2+1>
,
解得k<-
或k>
,
∴k的取值范围是(-∞,-
)∪(
,+∞).
|
解得a=2,b=1,
∴椭圆方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),AB中点(x0,y0),
由
|
∵直线:y=kx+m(k≠0)与椭圆C交于A,B两点,
∴△=64k2-16(4k2+1)(m2-1)>0,
解得4k2+1>m2,①
x1+x2=-
| 8km |
| 4k2+1 |
∴x0=-
| 4km |
| 4k2+1 |
| m |
| 4k2+1 |
由题意知DM垂直平分AB,∴DM的方程为x=-ky+1,
将点M的坐标代入,得m=-
| 4k2+1 |
| 3k |
由①②,得4k2+1>
| (4k2+1)2 |
| 9k |
解得k<-
| ||
| 5 |
| ||
| 5 |
∴k的取值范围是(-∞,-
| ||
| 5 |
| ||
| 5 |
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
| (lg9-1)2 |
| A、lg9-1 | ||
| B、1-lg9 | ||
| C、8 | ||
D、2
|
已知复数z=(1+i)(2-i)(i为虚数单位),则|z|=( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知三角函数f(x)=Asin(ωx+φ)+b同时满足以下三个条件:
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
+
,
则f(x)的单调区间为( )
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
| 1 |
| 2 |
| f(x)-f2(x) |
则f(x)的单调区间为( )
| A、[4k-1,4k+3],k∈Z |
| B、[4k+1,4k+3],k∈Z |
| C、[8k-2,8k+2],k∈Z |
| D、[8k+2,8k+6],k∈Z |
用反证法证明结论“?x0∈R”使得P(x0)成立,应假设( )
| A、?x0∈R,使得P(x0)不成立 |
| B、?x∈R,P(x)均成立 |
| C、?x∈R,P(x)均不成立 |
| D、不存在x0∈R,使得P(x0)不成立 |
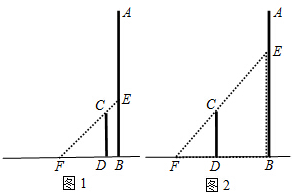 如图所示,直立在地面上的两根钢管AB和CD,AB=10
如图所示,直立在地面上的两根钢管AB和CD,AB=10