题目内容
若实数a,b,c满足a2+b2+c2=1,则3ab-3bc+2c2的最大值为 .
考点:柯西不等式在函数极值中的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:不妨考虑c,当c=0时,运用重要不等式a2+b2≥2ab,求得最大值;再由当c≠0时,3ab-3bc+2c2=
,
分子分母同除以c2,设x=
,y=
,再整理成二次方程,由于x为实数,运用判别式大于等于0,再由y为实数,判别式小于等于0,即可解得所求的范围,进而得到最大值.
| 3ab-3bc+2c2 |
| a2+b2+c2 |
分子分母同除以c2,设x=
| a |
| c |
| b |
| c |
解答:
解:不妨考虑c,当c=0时,有3ab-3bc+2c2=3ab≤
=
,
当c≠0时,3ab-3bc+2c2=
=
,
设x=
,y=
,则可令M=3ab-3bc+2c2=
,
即有Mx2-3xy+My2+M+3y-2=0,
由于x为实数,则有判别式△1=9y2-4M(My2+M+3y-2)≥0,
即有(9-4M2)y2-12My-4M(M-2)≥0,
由于y为实数,则△2=144M2+16M(9-4M2)(M-2)≤0,
即有M(M-3)(2M2+2M-3)≤0,
由于求M的最大值,则M>0,则M≤3.
故答案为:3.
| 3(a2+b2) |
| 2 |
| 3 |
| 2 |
当c≠0时,3ab-3bc+2c2=
| 3ab-3bc+2c2 |
| a2+b2+c2 |
3•
| ||||||
(
|
设x=
| a |
| c |
| b |
| c |
| 3xy-3y+2 |
| x2+y2+1 |
即有Mx2-3xy+My2+M+3y-2=0,
由于x为实数,则有判别式△1=9y2-4M(My2+M+3y-2)≥0,
即有(9-4M2)y2-12My-4M(M-2)≥0,
由于y为实数,则△2=144M2+16M(9-4M2)(M-2)≤0,
即有M(M-3)(2M2+2M-3)≤0,
由于求M的最大值,则M>0,则M≤3.
故答案为:3.
点评:本题考查重要不等式的运用:求最值,考查换元法转化为二次函数和二次方程有实根的条件,考查不等式的解法,属于压轴题和易错题.

练习册系列答案
相关题目
已知三角函数f(x)=Asin(ωx+φ)+b同时满足以下三个条件:
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
+
,
则f(x)的单调区间为( )
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
| 1 |
| 2 |
| f(x)-f2(x) |
则f(x)的单调区间为( )
| A、[4k-1,4k+3],k∈Z |
| B、[4k+1,4k+3],k∈Z |
| C、[8k-2,8k+2],k∈Z |
| D、[8k+2,8k+6],k∈Z |
用反证法证明结论“?x0∈R”使得P(x0)成立,应假设( )
| A、?x0∈R,使得P(x0)不成立 |
| B、?x∈R,P(x)均成立 |
| C、?x∈R,P(x)均不成立 |
| D、不存在x0∈R,使得P(x0)不成立 |
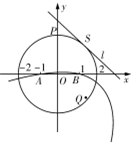 如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.
如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.