题目内容
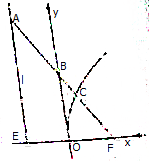 如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若
如图,过抛物线y2=2px(p>0)的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点,若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设C(x1,y1),直线AF与抛物线的另一个交点为(x2,y2).设直线AF的方程:y=k(x-
),与抛物线方程联立可得:k2x2-(pk2+2p)x+
p2=0,利用根与系数的关系及
=3
,xA=-
,xB=0,即可解出.
| p |
| 2 |
| k2 |
| 4 |
| AB |
| BC |
| P |
| 2 |
解答:
解:设C(x1,y1),直线AF与抛物线的另一个交点为(x2,y2).
设直线AF的方程:y=k(x-
),
联立
,化为:k2x2-(pk2+2p)x+
p2=0,
则x1+x2=
,x1x2=
.
∵
=3
,xA=-
,xB=0,
∴0+
=3x1,
∴x1=
.
∴x2=p+
-
=
+
.
∴
×(
+
)=
,
化为k2=3,
由图可知:k<0,
∴k=-
.
故选:A.
设直线AF的方程:y=k(x-
| p |
| 2 |
联立
|
| k2 |
| 4 |
则x1+x2=
| pk2+2p |
| k2 |
| p2 |
| 4 |
∵
| AB |
| BC |
| P |
| 2 |
∴0+
| p |
| 2 |
∴x1=
| p |
| 6 |
∴x2=p+
| 2p |
| k2 |
| p |
| 6 |
| 5p |
| 6 |
| 2p |
| k2 |
∴
| p |
| 6 |
| 5p |
| 6 |
| 2p |
| k2 |
| p2 |
| 4 |
化为k2=3,
由图可知:k<0,
∴k=-
| 3 |
故选:A.
点评:本题考查了直线与抛物线相交转化为方程联立可得根与系数的关系、向量的坐标运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知1∈{a,a+1,a2},则实数a的可取值是( )
| A、0 | B、1 |
| C、-1 | D、0或1或-1 |
用反证法证明结论“?x0∈R”使得P(x0)成立,应假设( )
| A、?x0∈R,使得P(x0)不成立 |
| B、?x∈R,P(x)均成立 |
| C、?x∈R,P(x)均不成立 |
| D、不存在x0∈R,使得P(x0)不成立 |
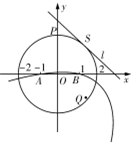 如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.
如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.