题目内容
已知非零向量
、
不共线，如果
=
+
，
=2
+8
，
=3
-3
，求证：A、B、C、D共面．
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| AC |
| e1 |
| e2 |
| AD |
| e1 |
| e2 |
考点：平面向量的基本定理及其意义
专题：空间向量及应用
分析：设
=λ
+μ
，根据平面向量基本定理便可求出λ，μ，所以根据空间向量共面的充要条件即可得到
，
，
三向量共面，所以A，B，C，D共面．
| AB |
| AC |
| AD |
| AB |
| AC |
| AD |
解答：
证明：假设
=λ
+μ
，λ，μ∈R；
∴
+
=λ(2
+8
)+μ(3
-3
)；
整理得：(1-2λ-3μ)
+(1-8λ+3μ)
=
；
∵
，
不共线；
∴
；
解得λ=
，μ=
；
∴
=
+
；
∵
，
不共线；
∴根据空间向量共面的充要条件即知
，
，
三向量共面；
∴A，B，C，D共面．
| AB |
| AC |
| AD |
∴
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
整理得：(1-2λ-3μ)
| e1 |
| e2 |
| 0 |
∵
| e1 |
| e2 |
∴
|
解得λ=
| 1 |
| 10 |
| 4 |
| 15 |
∴
| AB |
| 1 |
| 10 |
| AC |
| 4 |
| 15 |
| AD |
∵
| AC |
| AD |
∴根据空间向量共面的充要条件即知
| AB |
| AC |
| AD |
∴A，B，C，D共面．
点评：平面向量基本定理，以及空间向量共面的充要条件．
练习册系列答案
相关题目
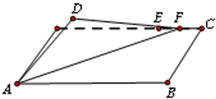如图，在长方形ABCD中，AB=4，BC=1，E为DC的四等分点（靠近C处），F为线段EC上一动点（包括端点），现将△AFD沿AF折起，使D点在平面内的射影恰好落在边AB上，则当F运动时，二面角D-AF-B的平面角余弦值的变化范围为