题目内容
已知等差数列{bn}的前n项和为Sn,且b1=
+1,S3=3
+6
(1)求数列{bn}的通项公式;
(2)证明数列{bn}中任意不同的三项都不可能成为等比数列.
| 2 |
| 2 |
(1)求数列{bn}的通项公式;
(2)证明数列{bn}中任意不同的三项都不可能成为等比数列.
考点:等比关系的确定,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)根据等差数列的通项公式即可求数列{bn}的通项公式;
(2)根据等比数列的定义建立方程关系,即可证明数列{bn}中任意不同的三项都不可能成为等比数列.
(2)根据等比数列的定义建立方程关系,即可证明数列{bn}中任意不同的三项都不可能成为等比数列.
解答:
解:(1)设等差数列的公差为d,
则S3=3
+6=3(
+1)+
d=3(
+1)+3d,
解得d=
=
=1,
即数列{bn}的通项公式为
+1+(n-1)=n+
;
(2)若数列{bn}中任意的三项bn-1,bn,bn+1都成为等比数列.
则bn2=bn-1bn+1,
即(n+
)2=(n-1+
)(n+1+
)=[n+(
-1)][n+(
+1)],
展开得n2+2
n+2=n2+2
n+1,
即2=1,则方程不成立,
故数列{bn}中任意不同的三项都不可能成为等比数列.
则S3=3
| 2 |
| 2 |
| 3×2 |
| 2 |
| 2 |
解得d=
3
| ||||
| 3 |
| 3 |
| 3 |
即数列{bn}的通项公式为
| 2 |
| 2 |
(2)若数列{bn}中任意的三项bn-1,bn,bn+1都成为等比数列.
则bn2=bn-1bn+1,
即(n+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
展开得n2+2
| 2 |
| 2 |
即2=1,则方程不成立,
故数列{bn}中任意不同的三项都不可能成为等比数列.
点评:本题主要考查等差数列和等比数列的应用,根据等差数列和等比数列的通项公式是解决本题的关键.

练习册系列答案
相关题目
已知平面向量
,
,|
|=2,
=(2,
),若|
-
|=
,则
•
的值是( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=x3-3x+m恰有2个不同的零点,则实数m的值为( )
| A、±2 | B、±1 |
| C、-2或1 | D、-1或2 |
 ,若在区间
,若在区间 上,不等式
上,不等式 恒成立,则实数
恒成立,则实数 的取值范围为__________。
的取值范围为__________。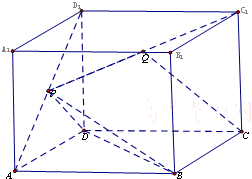 如图,在正方体ABCD-A1B1C1D1中,P为线段AD1上的中点,Q为线段PC1上的中点.
如图,在正方体ABCD-A1B1C1D1中,P为线段AD1上的中点,Q为线段PC1上的中点.