题目内容
若函数f(x)=x3-3x+m恰有2个不同的零点,则实数m的值为( )
| A、±2 | B、±1 |
| C、-2或1 | D、-1或2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:先求出函数的导数,得到函数的单调区间,从而求出m的值.
解答:
解:∵f′(x)=3(x2-1),
∴f(x)在(-∞,-1),(1,+∞)上都递增,在[-1,1]上递减,
因此要使f(x)恰有2个零点,
则只需f(-1)=0或f(1)=0,
∴m=±2.
故选:A
∴f(x)在(-∞,-1),(1,+∞)上都递增,在[-1,1]上递减,
因此要使f(x)恰有2个零点,
则只需f(-1)=0或f(1)=0,
∴m=±2.
故选:A
点评:本题考查了函数的单调性,考查了函数的零点问题,是一道基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0<0,则a的取值范围是( )
| A、(2,+∞) |
| B、(1,+∞) |
| C、(-∞,-2) |
| D、(-∞,-1) |
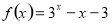 的一个零点所在的区间为( )
的一个零点所在的区间为( )