题目内容
证明：logn（n+1）＞log（n+1）（n+2）．
考点：不等式的证明
专题：推理和证明
分析：由n＞1，可得logn（n+1）＞0，logn+1（n+2）＞0，且logn（n+1）≠logn+1（n+2），再利用基本不等式即可证明．
解答：
证明：∵n＞1，∴logn（n+1）＞0，logn+1（n+2）＞0，且logn（n+1）≠logn+1（n+2），
∴logn+1nlogn+1（n+2）＜[
]2=[
]2＜1，
∴当n＞1时，logn+1nlogn+1（n+2）＜1，
∴logn（n+1）＞logn+1（n+2）．
∴logn+1nlogn+1（n+2）＜[
| logn+1n+logn+1(n+2) |
| 2 |
| logn+1(n2+2n) |
| 2 |
∴当n＞1时，logn+1nlogn+1（n+2）＜1，
∴logn（n+1）＞logn+1（n+2）．
点评：本题考查了对数函数的性质和基本不等式的应用，深刻理解以上知识及放缩法是解决问题的关键．
练习册系列答案
相关题目
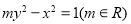与椭圆
有相同的焦点，则该双曲线的渐近线方程为（ ）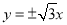
（B）
（C）
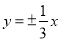（D）