题目内容
17.已知向量$\overrightarrow a=(1,2),|\overrightarrow b|=1$,且$\overrightarrow a$与$\overrightarrow b$的夹角为60°.(1)求与$\overrightarrow a$垂直的单位向量的坐标;
(2)求向量$2\overrightarrow b-\overrightarrow a$在$\overrightarrow a$上的投影.
分析 (1)设与$\overrightarrow a$垂直的单位向量为$\overrightarrow{c}$=(x,y),则$\left\{\begin{array}{l}{\overrightarrow{a}•\overrightarrow{c}=0}\\{|\overrightarrow{c}|=1}\end{array}\right.$,列方程组求出x、y的值即可;
(2)根据平面向量投影的定义,利用数量积与夹角公式计算即可.
解答 解:向量$\overrightarrow a=(1,2),|\overrightarrow b|=1$,且$\overrightarrow a$与$\overrightarrow b$的夹角θ为60°.
(1)设与$\overrightarrow a$垂直的单位向量为$\overrightarrow{c}$=(x,y),
则$\left\{\begin{array}{l}{\overrightarrow{a}•\overrightarrow{c}=0}\\{|\overrightarrow{c}|=1}\end{array}\right.$,
即$\left\{\begin{array}{l}{x+2y=0}\\{{x}^{2}{+y}^{2}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2\sqrt{5}}{5}}\\{y=-\frac{\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{2\sqrt{5}}{5}}\\{y=\frac{\sqrt{5}}{5}}\end{array}\right.$;
∴$\overrightarrow{c}$=($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$)或$\overrightarrow{c}$=(-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$);
(2)∵(2$\overrightarrow{b}$-$\overrightarrow{a}$)•$\overrightarrow{a}$=2$\overrightarrow{a}$•$\overrightarrow{b}$-${\overrightarrow{a}}^{2}$
=2×$\sqrt{{1}^{2}{+2}^{2}}$×1×cos60°-(12+22)
=$\sqrt{5}$-5,
|$\overrightarrow{a}$|=$\sqrt{5}$,
∴向量$2\overrightarrow b-\overrightarrow a$在$\overrightarrow a$上的投影为:
|$\overrightarrow{2b}$-$\overrightarrow{a}$|cos<2$\overrightarrow{b}$-$\overrightarrow{a}$,$\overrightarrow{a}$>=$\frac{(2\overrightarrow{b}-\overrightarrow{a})•\overrightarrow{a}}{|\overrightarrow{a}|}$=$\frac{\sqrt{5}-5}{\sqrt{5}}$=1-$\sqrt{5}$.
点评 本题考查了解方程组以及平面向量投影的定义与应用问题,是综合题.

 阅读快车系列答案
阅读快车系列答案| A. | $2\sqrt{3}-5$ | B. | $2\sqrt{3}-2$ | C. | $5\sqrt{3}+1$ | D. | $2\sqrt{3}+1$ |
| A. | 120 | B. | 130 | C. | 90 | D. | 109 |
| A. | 闭区间上函数极大值一定比极小值大 | |
| B. | 闭区间上函数最大值一定是极大值 | |
| C. | 若|p|<$\sqrt{6}$,则f(x)=x3+px2+2x+1无极值 | |
| D. | 函数f(x)在区间(a,b)上一定存在最值 |
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
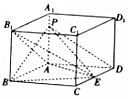 如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |