题目内容
7.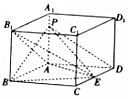 如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 在棱AB上取点M,使得BM=1,
过点M作MN∥BB1,交AB1于N,连接EM、EN,
证明平面EMN∥平面ADD1A1,求出MN的值,
由AP=MN得出DP∥平面AEB;
再取DG=AP,连接CG,利用平行关系求出DF的长.
解答 解:在长方体ABCD-A1B1C1D1的棱AB上取点M,使得BM=1,
过点M作MN∥BB1,交AB1于N,连接EM、EN,如图所示;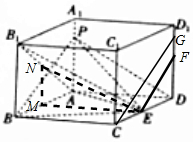
则平面EMN∥平面ADD1A1;
∵BB1=2AM=2BM,
∴MN=$\frac{4}{3}$,
∴当AP=MN=$\frac{4}{3}$时,DP∥EN,
即DP∥平面AEB1;
∵F是棱DD1与平面BEP的交点,
∴EF∥BP;
取DG=AP=$\frac{4}{3}$,连接CG,则CG∥BP,
∴EF∥CG,
∴DF=$\frac{2}{3}$DG=$\frac{8}{9}$.
故选:B.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了求线段长的应用问题,是综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一个样本a,3,4,5,6的平均数为b,且方程x2-6x+c=0的两个根为a,b,则该样本的方差为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
2.某三棱锥的三视图如图所示,则俯视图的面积为( )
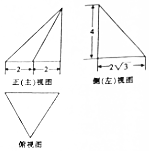

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
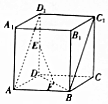 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.