题目内容
已知椭圆
+
=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=2
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线y=kx+m相交于不同的两点M、N,又点A(0,-1),当|AM|=|AN|时,求实数m的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求椭圆方程;
(2)设椭圆与直线y=kx+m相交于不同的两点M、N,又点A(0,-1),当|AM|=|AN|时,求实数m的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)利用|F1F2|=2
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.列出方程组求出a、b即可求得椭圆方程.
(2)当k=0时,直线和椭圆有两交点只需-1<m<1;当k≠0时,设弦MN的中点为P(xp,yp),xM、xN分别为点M、N的横坐标,联立直线方程与椭圆方程,利用直线与椭圆有两个不同的交点,得到△>0,可得m2<3k2+1,通过|AM|=|AN|,判断AM⊥AN,得到2m=3k2+1,然后求得m的取值范围.
| 2 |
(2)当k=0时,直线和椭圆有两交点只需-1<m<1;当k≠0时,设弦MN的中点为P(xp,yp),xM、xN分别为点M、N的横坐标,联立直线方程与椭圆方程,利用直线与椭圆有两个不同的交点,得到△>0,可得m2<3k2+1,通过|AM|=|AN|,判断AM⊥AN,得到2m=3k2+1,然后求得m的取值范围.
解答:
解:(1)由已知,可得c=
,a=
b,
∵a2=b2+c2,∴a=
,b=1,
∴
+y2=1.…(4分)
(2)当k=0时,直线和椭圆有两交点只需-1<m<1; …(5分)
当k≠0时,设弦MN的中点为P(xp,yp),xM、xN分别为点M、N的横坐标,由
,得(3k2+1)x2+6mkx+3(m2-1)=0,
由于直线与椭圆有两个不同的交点,所以
∴△>0,即m2<3k2+1 ①…(7分)
xp=
=-
,从而yp=kxp+m=
,kAP=
=-
…(9分)
又|AM|=|AN|∴AM⊥AN,则-
=-
,即2m=3k2+1 ②,…(10分)
将②代入①得2m>m2,解得0<m<2,由②得k2=
>0,解得m>
,
故所求的m取值范围是(
,2).…(12分)
∴当k≠0时,m的取值范围是(
,2).
当k=0时,m的取值范围是(-1,1)…(13分)
| 2 |
| 3 |
∵a2=b2+c2,∴a=
| 3 |
∴
| x2 |
| 3 |
(2)当k=0时,直线和椭圆有两交点只需-1<m<1; …(5分)
当k≠0时,设弦MN的中点为P(xp,yp),xM、xN分别为点M、N的横坐标,由
|
由于直线与椭圆有两个不同的交点,所以
∴△>0,即m2<3k2+1 ①…(7分)
xp=
| xM+xN |
| 2 |
| 3mk |
| 3k2+1 |
| mk |
| 3k2+1 |
| yp+1 |
| xP |
| m+3k2+1 |
| 3mk |
又|AM|=|AN|∴AM⊥AN,则-
| m+3k2+1 |
| 3mk |
| 1 |
| k |
将②代入①得2m>m2,解得0<m<2,由②得k2=
| 2m-1 |
| 3 |
| 1 |
| 2 |
故所求的m取值范围是(
| 1 |
| 2 |
∴当k≠0时,m的取值范围是(
| 1 |
| 2 |
当k=0时,m的取值范围是(-1,1)…(13分)
点评:本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,求解范围问题,一般通过含变量一个方程与一个不等式的关系求解.

练习册系列答案
相关题目
在△ABC中,点M是BC中点.若∠A=120°,
•
=-
,则|
|的最小值是( )
| AB |
| AC |
| 1 |
| 2 |
| AM |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
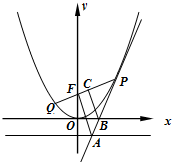 已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.
已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.