题目内容
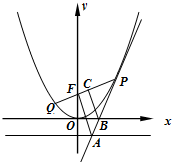 已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.
已知抛物线C:x2=4y的焦点为F,P是抛物线上异于原点的任意一点,直线PF与抛物线另一交点为点Q,设l是过点P的抛物线的切线,l与直线y=-1和x轴的交点分别为A,B.(1)求证:AF⊥PQ;
(2)过B作BC⊥PQ于C,若|PC|=|QF|,求|PQ|.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(m,
),过P的切线方程为:y=
x-
,分别求出A和F的坐标,由此利用向量的计算公式能证明AF⊥PQ.
(2)分别过B、P作直线y=-1的垂线,垂足为D、E,由已知条件推导出|FC|=|BD|=1,设直线PQ的方程为y=kx+1,代入C:x2=4y得x2-4kx-4=0,由此能求出|PQ|的长.
| m2 |
| 4 |
| m |
| 2 |
| m2 |
| 4 |
(2)分别过B、P作直线y=-1的垂线,垂足为D、E,由已知条件推导出|FC|=|BD|=1,设直线PQ的方程为y=kx+1,代入C:x2=4y得x2-4kx-4=0,由此能求出|PQ|的长.
解答:
(1)证明:设P(m,
),
则过P的切线方程为:y=
x-
,┅(2分)
由
,得A的坐标(
-
,-1),
又∵抛物线C:x2=4y的焦点为F(0,1),
∴
=(m,
-1),
=(
,-2),┅(4分)
∴
•
=m•
+(
-1)•(-2)=0,┅(6分)
∴AF⊥PQ.┅(7分)
(2)解:分别过B、P作直线y=-1的垂线,垂足为D、E,
∵BC∥AF,∴
=
=
,
∵|FP|=|PE|,∴|FC|=|BD|=1,┅(9分)
设直线PQ的方程为y=kx+1,代入C:x2=4y得x2-4kx-4=0,
∴m•xQ=-4,∴xQ=-
,∴yQ=
,┅(11分)
∵|PF|=
+1,|QF|=
+1,∴|PC|=
,
由|PC|=|QF|,得
+1=
,
∴m4-4m2-16=0,解得m2=2+2
,┅(14分)
∴|PQ|=
+
+2=
+2.┅(15分)
| m2 |
| 4 |
则过P的切线方程为:y=
| m |
| 2 |
| m2 |
| 4 |
由
|
| m |
| 2 |
| 2 |
| m |
又∵抛物线C:x2=4y的焦点为F(0,1),
∴
| FP |
| m2 |
| 4 |
| FA |
| m2-4 |
| 2m |
∴
| FP |
| FA |
| m2-4 |
| 2m |
| m2 |
| 4 |
∴AF⊥PQ.┅(7分)
(2)解:分别过B、P作直线y=-1的垂线,垂足为D、E,
∵BC∥AF,∴
| |FC| |
| |FP| |
| |AB| |
| |AP| |
| |BD| |
| |PE| |
∵|FP|=|PE|,∴|FC|=|BD|=1,┅(9分)
设直线PQ的方程为y=kx+1,代入C:x2=4y得x2-4kx-4=0,
∴m•xQ=-4,∴xQ=-
| 4 |
| m |
| 4 |
| m2 |
∵|PF|=
| m2 |
| 4 |
| 4 |
| m2 |
| m2 |
| 4 |
由|PC|=|QF|,得
| 4 |
| m2 |
| m2 |
| 4 |
∴m4-4m2-16=0,解得m2=2+2
| 5 |
∴|PQ|=
| m2 |
| 4 |
| 4 |
| m2 |
| 5 |
点评:本题考查直线垂直的证明,考查线段长的求法,解题时要认真审题,注意函数与方程思想、等价转化思想的合理运用.

练习册系列答案
相关题目
设i为虚数单位,则复数z=
在复平面内所对应的点位于( )
| 3-4i |
| i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |