题目内容
给出下列四个命题:
(1)平面内的一条直线与平面外的一条直线是异面直线;
(2)若三个平面两两相交,则这三个平面把空间分成7部分;
(3)用一个面去截棱锥,底面与截面之间的部分叫棱台;
(4)一条直线与两条异面直线中的一条直线相交,那么它和另一条直线可能相交、平行或异面.
其中真命题的个数是( )
(1)平面内的一条直线与平面外的一条直线是异面直线;
(2)若三个平面两两相交,则这三个平面把空间分成7部分;
(3)用一个面去截棱锥,底面与截面之间的部分叫棱台;
(4)一条直线与两条异面直线中的一条直线相交,那么它和另一条直线可能相交、平行或异面.
其中真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:(1)写出平面内的一条直线与平面外的一条直线的位置关系,即可判定命题正误;
(2)画出三个平面两两相交的情况,即可判定命题的正误;
(3)根据棱台的定义,可以判定命题的正误;
(4)举例说明命题是正确的.
(2)画出三个平面两两相交的情况,即可判定命题的正误;
(3)根据棱台的定义,可以判定命题的正误;
(4)举例说明命题是正确的.
解答:
解:(1)平面内的一条直线与平面外的一条直线的位置关系是平行,相交,或异面;
∴命题(1)错误;
(2)三个平面两两相交,这三个平面可以把空间分成6或7部分,
如图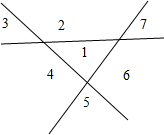 ,
,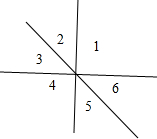 ;
;
∴命题(2)错误;
(3)用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台;
∴命题(3)错误;
(4)一条直线与两条异面直线中的一条直线相交,
那么它和另一条直线可能相交(如两条异面直线的公垂线),
平行(如作两条异面直线所成的角),
或异面(如正方体中下底面的对角线与上底面的棱);
∴命题(4)正确;
所以,以上真命题只有1个,是(4);
故选:B.
∴命题(1)错误;
(2)三个平面两两相交,这三个平面可以把空间分成6或7部分,
如图
 ,
, ;
;∴命题(2)错误;
(3)用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台;
∴命题(3)错误;
(4)一条直线与两条异面直线中的一条直线相交,
那么它和另一条直线可能相交(如两条异面直线的公垂线),
平行(如作两条异面直线所成的角),
或异面(如正方体中下底面的对角线与上底面的棱);
∴命题(4)正确;
所以,以上真命题只有1个,是(4);
故选:B.
点评:本题通过命题真假的判定考查了空间中的两条直线的位置关系、平面与平面的相交以及棱台的概念等问题,是综合性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
i•z=1-i(i为虚数单位),则z=( )
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
设i为虚数单位,则复数z=
在复平面内所对应的点位于( )
| 3-4i |
| i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
下列命题的说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为:“x≠1,则x2-3x+2≠0”. |
| B、“x=1是“x2-3x+2=0”的充分不必要条件. |
| C、对于命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,x02+x0+1≤0. |
| D、若p∧q为假命题,则p、q均为假命题. |
 如图,正方形CDEF内接于椭圆
如图,正方形CDEF内接于椭圆