题目内容
18.已知f(x)=3sin(2x+$\frac{π}{4}$)-1.(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
分析 (1)由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
(2)由条件利用正弦函数的周期性、正弦函数的图象的对称性、单调性即可得解.
解答 解:(1)将函数y=sin x图象上每一点的横坐标不变,纵坐标伸长到原来的3倍得到函数y=3sinx的图象,
再把所得函数图象上每一点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),得到函数y=3sin2x的图象,
再把所得函数的图象向左平移$\frac{π}{8}$个单位长度,得到函数y=3sin(2x+$\frac{π}{4}$) 的图象,
再把所得函数的图象向下平移1个单位长度,得到函数f(x)=3sin(2x+$\frac{π}{4}$)-1的图象.
(2)对于函数f(x)=3sin(2x+$\frac{π}{4}$)-1,它的最小正周期为$\frac{2π}{2}$=π,
由2x+$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈Z,求得x=$\frac{1}{2}$kπ+$\frac{π}{8}$,可得函数的图象的对称轴方程为x=$\frac{1}{2}$kπ+$\frac{π}{8}$,k∈Z.
由2x+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z,求得x=kπ+$\frac{π}{8}$,可得当x=kπ+$\frac{π}{8}$,k∈Z时,f(x)的最大值为3-1=2.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,考查正弦函数的周期性、正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
8.已知双曲线与 椭圆x2+4y2=64共焦点,它的一条渐近线方程为$x-\sqrt{3}y=0$,则双曲线的方程为$\frac{{x}^{2}}{36}-\frac{{y}^{2}}{12}=1$.
10.已知椭圆与双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$有共同的焦点,且离心率为$\frac{{\sqrt{5}}}{5}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
7.已知$\frac{sinα-2cosα}{2sinα+3cosα}=2$,那么tanα的值为( )
| A. | -2 | B. | $-\frac{8}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
8.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
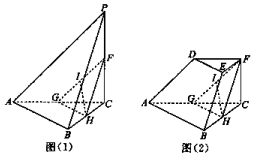 如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.
如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.