题目内容
7.已知$\frac{sinα-2cosα}{2sinα+3cosα}=2$,那么tanα的值为( )| A. | -2 | B. | $-\frac{8}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
分析 原式分子分母同除以cosα,利用同角三角函数间的基本关系弦化切后,变形即可求出tanα的值.
解答 解:$\frac{sinα-2cosα}{2sinα+3cosα}$=$\frac{tanα-2}{2tanα+3}$=2,解得tanα=$-\frac{8}{3}$.
故选:B.
点评 本题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.从2013年1月1号开始,铁道部对火车票大面积降价,但降价幅度引发了争议.于是,某高校对此展开了一项调查,得到如下数据:
若从参与调查的人员中,按分层抽样的方法抽取50人进行座谈,则给出“差评”与“好评”的人数之差为( )
| 对此事的态度 | 好评(有利于百姓出行) | 中评(影响不大) | 差评(纯属忽悠) | 不关心 |
| 人数 | 2000 | 4000 | 3000 | 1000 |
| A. | 10 | B. | 8 | C. | 5 | D. | 3 |
18.已知f(x)=3sin(2x+$\frac{π}{4}$)-1.
(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
16.当$x=\frac{π}{4}$时,函数f(x)=sin(ωx+φ)(A>0)取得最小值,则函数$y=f({\frac{3π}{4}-x})$是( )
| A. | 奇函数且图象关于点$({\frac{π}{2},0})$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D. | 偶函数且图象关于点$({\frac{π}{2},0})$对称 |
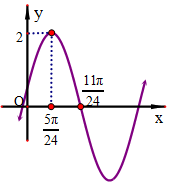 已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.