题目内容
13.在△ABC中,角A,B,C的对边分别为a,b,c,$cosC=\frac{3}{10}$.(1)若$\overrightarrow{CA}•\overrightarrow{CB}=\frac{9}{2}$,求△ABC的面积;
(2)设向量$\overrightarrow x=(2sinB,-\sqrt{3})$,$\overrightarrow y=(cos2B,1-2{sin^2}\frac{B}{2})$,且$\overrightarrow x∥\overrightarrow y$,求角B的值.
分析 (1)根据题意,由平面向量的数量积的计算公式,变形化简可得ab=15,借助三角函数基本关系计算可得sinC的值,由三角形面积公式计算可得答案;
(2)由向量平行的坐标计算公式可得2sinB(1-2sin2$\frac{B}{2}$)-(-$\sqrt{3}$)cos2B=0,化简可得$sin2B+\sqrt{3}cos2B=0$,进而可得$tan2B=-\sqrt{3}$,即可得B的值,分析B、C的大小关系,可得答案.
解答 解:(1)根据题意,∵$\overrightarrow{CB}•\overrightarrow{CA}=\frac{9}{2}$,∴$abcosC=\frac{9}{2}$,∴ab=15,
又∵$cosC=\frac{3}{10}$,C∈(0,π),$sinC=\frac{{\sqrt{91}}}{10}$.
所以${S_{△ABC}}=\frac{{3\sqrt{91}}}{4}$.
(2)根据题意,∵$\overrightarrow x∥\overrightarrow y$,∴2sinB(1-2sin2$\frac{B}{2}$)-(-$\sqrt{3}$)cos2B=0,
即$2sinB[{1-2{{sin}^2}\frac{B}{2}}]+\sqrt{3}cos2B=0$,
$2sinBcosB+\sqrt{3}cos2B=0$,即$sin2B+\sqrt{3}cos2B=0$,显然cos2B≠0,
所以$tan2B=-\sqrt{3}$,
所以$2B=\frac{2π}{3}$或$\frac{5π}{3}$,即$B=\frac{π}{3}$或$\frac{5π}{6}$,
因为$cosC=\frac{3}{10}$$<\frac{{\sqrt{3}}}{2}$,所以$C>\frac{π}{6}$,
所以$B=\frac{5π}{6}$(舍去),
即$B=\frac{π}{3}$.
点评 本题靠三角形中的几何计算,涉及向量的数量积运算以及向量平行的坐标表示,(2)中注意取舍.

| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
| A. | $\frac{3}{2}$ | B. | $\frac{14}{13}$ | C. | $\frac{56}{41}$ | D. | $\frac{29}{23}$ |
| A. | 70πcm2 | B. | 70 cm2 | C. | 80cm2 | D. | 80πcm2 |
(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
| A. | (0,4) | B. | (0,3) | C. | (0,2) | D. | (0,1) |
| A. | 1 | B. | 4 | C. | -1 | D. | 0 |
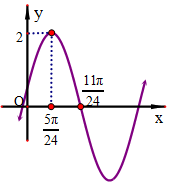 已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.