题目内容
8.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 求出抛物线的准线方程,利用抛物线的定义转化求解即可.
解答 解:抛物线y2=4x的准线方程为:x=-1,抛物线y2=4x上的点M到焦点的距离为10,
可得xM=9,则M到y轴的距离是:9.
故选:D.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
18.已知f(x)=3sin(2x+$\frac{π}{4}$)-1.
(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
(1)f(x)的图象是由y=sin x的图象如何变换而来?
(2)求f(x)的最小正周期、图象的对称轴方程、最大值及其对应的x的值.
16.当$x=\frac{π}{4}$时,函数f(x)=sin(ωx+φ)(A>0)取得最小值,则函数$y=f({\frac{3π}{4}-x})$是( )
| A. | 奇函数且图象关于点$({\frac{π}{2},0})$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D. | 偶函数且图象关于点$({\frac{π}{2},0})$对称 |
3.已知函数f(x)=ax3+c,且f′(1)=6,函数在[1,2]上的最大值为20,则c的值为( )
| A. | 1 | B. | 4 | C. | -1 | D. | 0 |
20.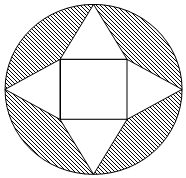 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
 如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.
如图所示,从一个半径(1+$\sqrt{3}$)m的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥,则该四棱锥的体积是( )m3.| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{6}$ |
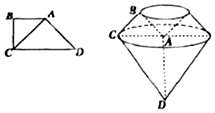 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体. 如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.