题目内容
4.在平面直角坐标系xOy中,若双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)经过抛物线y2=8x的焦点,则该双曲线的离心率是$\frac{\sqrt{5}}{2}$.分析 根据题意,由抛物线的方程可得其焦点坐标,将其代入双曲线的方程可得a2的值,即可得双曲线的方程,计算可得c的值,由双曲线离心率公式计算可得答案.
解答 解:根据题意,抛物线的方程为y2=8x,
其焦点为(2,0),
若双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)经过点(2,0),
则有$\frac{4}{{a}^{2}}$-0=1,解可得a2=4,
即双曲线的方程为:$\frac{{x}^{2}}{4}$-y2=1,
则a=2,c=$\sqrt{4+1}$=$\sqrt{5}$,
则双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$;
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查双曲线、抛物线的几何性质,注意由抛物线的几何性质求出其焦点坐标.

练习册系列答案
相关题目
1.若P为可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
19.设x,y满足$\left\{\begin{array}{l}{x≥0}\\{x+y-2≤0}\\{ax-y-a≤0}\end{array}\right.$,若z=2x+y的最大值为$\frac{7}{2}$,则a的值为( )
| A. | $-\frac{7}{2}$ | B. | 0 | C. | 1 | D. | $-\frac{7}{2}$或1 |
14.如图,已知$\overrightarrow{AB}=a$,$\overrightarrow{AC}=b$,$\overrightarrow{DC}=3\overrightarrow{BD}$,$\overrightarrow{AE}=2\overrightarrow{EC}$,则$\overrightarrow{DE}$=( )
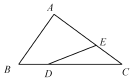

| A. | $\frac{3}{4}b-\frac{1}{3}a$ | B. | $\frac{5}{12}a-\frac{3}{4}b$ | C. | $\frac{3}{4}a-\frac{1}{3}b$ | D. | $\frac{5}{12}b-\frac{3}{4}a$ |
