题目内容
9.如图,半圆AOB是某爱国主义教育基地一景点的平面示意图,半径OA的长为1百米.为了保护景点,基地管理部门从道路l上选取一点C,修建参观线路C-D-E-F,且CD,DE,EF均与半圆相切,四边形CDEF是等腰梯形,设DE=t百米,记修建每1百米参观线路的费用为f(t)万元,经测算f(t)=$\left\{\begin{array}{l}{5,0<t≤\frac{1}{3}}\\{8-\frac{1}{t},\frac{1}{3}<t<2}\end{array}\right.$
(1)用t表示线段EF的长;
(2)求修建参观线路的最低费用.
分析 (1)设DQ与半圆相切于点Q,则由四边形CDEF是等腰梯形知,OQ⊥DE,以CF所在直线为x轴,OQ所在直线为y轴,建立平面直角坐标系xoy.设EF与圆切于G点,连接OG,过点E作EH⊥OF,垂足为H.可得Rt△EHF≌Rt△OGF,HF=FG=EF-$\frac{1}{2}$t.利用EF2=1+HF2=1+$(EF-\frac{1}{2}t)^{2}$,解得EF.
(2)设修建该参观线路的费用为y万元.
①当$0<t≤\frac{1}{3}$,由y=5$[2(\frac{t}{4}+\frac{1}{t})+t]$=5$(\frac{3}{2}t+\frac{2}{t})$.利用y′,可得y在$(0,\frac{1}{3}]$上单调递减,即可得出y的最小值.
②当$\frac{1}{3}<t<2$时,y=$(8-\frac{1}{t})$$[2(\frac{t}{4}+\frac{1}{t})+t]$=12t+$\frac{16}{t}$-$\frac{3}{2}$-$\frac{2}{{t}^{2}}$.利用导数研究函数的单调性极值最值即可得出.
解答 解:(1)设DQ与半圆相切于点Q,则由四边形CDEF是等腰梯形知,OQ⊥DE,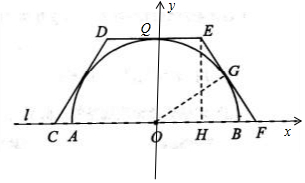
以CF所在直线为x轴,OQ所在直线为y轴,
建立平面直角坐标系xoy.
设EF与圆切于G点,连接OG,过点E作EH⊥OF,垂足为H.
∵EH=OG,∠OFG=∠EFH,∠GOF=∠HEF,
∴Rt△EHF≌Rt△OGF,∴HF=FG=EF-$\frac{1}{2}$t.
∴EF2=1+HF2=1+$(EF-\frac{1}{2}t)^{2}$,
解得EF=$\frac{t}{4}$+$\frac{1}{t}$(0<t<2).
(2)设修建该参观线路的费用为y万元.
①当$0<t≤\frac{1}{3}$,由y=5$[2(\frac{t}{4}+\frac{1}{t})+t]$=5$(\frac{3}{2}t+\frac{2}{t})$.y′=$5(\frac{3}{2}-\frac{2}{{t}^{2}})$<0,可得y在$(0,\frac{1}{3}]$上单调递减,
∴t=$\frac{1}{3}$时,y取得最小值为32.5.
②当$\frac{1}{3}<t<2$时,y=$(8-\frac{1}{t})$$[2(\frac{t}{4}+\frac{1}{t})+t]$=12t+$\frac{16}{t}$-$\frac{3}{2}$-$\frac{2}{{t}^{2}}$.
y′=12-$\frac{16}{{t}^{2}}$+$\frac{2}{{t}^{3}}$=$\frac{4(t-1)(3{t}^{2}+3t-1)}{{t}^{3}}$.
∵$\frac{1}{3}<t<2$,∴3t2+3t-1>0.
∴t∈$(\frac{1}{3},1)$时,y′<0,函数y此时单调递减;t∈(1,2)时,y′>0,函数y此时单调递增.
∴t=1时,函数y取得最小值24.5.
由 ①②知,t=1时,函数y取得最小值为24.5.
答:(1)EF=$\frac{t}{4}$+$\frac{1}{t}$(0<t<2)(百米).(2)修建该参观线路的最低费用为24.5万元.
点评 本题考查了利用导数研究函数的极值与最值、不等式的性质、直线与圆相切的性质,考查了推理能力与计算能力,属于中档题.

| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
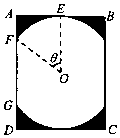 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$,设∠EOF=θ,透光区域的面积为S.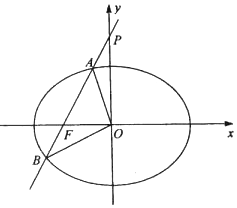 已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.
已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.