题目内容
16.已知曲线C的极坐标方程为ρ=6sinθ,以极点O为原点,极轴为x轴的非负半轴建立直角坐标系,直线l的参数方程为$\left\{\begin{array}{l}x=1+at\\ y=2+t\end{array}\right.$(t为参数).
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)直线l与曲线C交于B,D两点,当|BD|取到最小值时,求a的值.
分析 (1)曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方可得圆心C(0,3),半径r=3.直线l的参数方程为$\left\{\begin{array}{l}{x=1+at}\\{y=2+t}\end{array}\right.$(t为参数),消去参数t可得普通方程.
(2)由直线l经过定点P(1,2),此点在圆的内部,因此当CP⊥l时,|BD|取到最小值,利用相互垂直的直线斜率之间的关系可得k1,即可得出.
解答 解:(1)曲线C的极坐标方程为ρ=6sinθ,即ρ2=6ρsinθ,
化为直角坐标方程:x2+y2=6y,配方为:x2+(y-3)2=9,圆心C(0,3),半径r=3.
直线l的参数方程为$\left\{\begin{array}{l}{x=1+at}\\{y=2+t}\end{array}\right.$(t为参数),消去参数t可得:x-ay+2a-1=0.
(2)由直线l经过定点P(1,2),此点在圆的内部,
因此当CP⊥l时,|BD|取到最小值,则${k_{CP}}•{k_1}=\frac{2-3}{1-0}×{k_1}=-1$,解得k1=1.
∴$\frac{1}{a}=1$,解得a=1.
点评 本题考查了极坐标化为直角坐标方程、参数方程化为普通方程及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方式,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的2×2列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
(2)若从年龄在[55,65),[65,75)的别调查的人中各随机选取两人进行追踪调查,记选中的4人中赞成“使用微信交流”的人数为X,求随机变量X的分布列及数学期望.
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
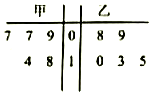 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.