题目内容
12.已知点M,N是抛物线C:y=4x2上不同的两点,F为抛物线C的焦点,且满足∠MFN=135°,弦MN的中点P到C的准线l的距离记为d,若|MN|2=λ•d2,则λ的最小值为2+$\sqrt{2}$.分析 求得抛物线的焦点和准线方程,设|MF|=a,|NF|=b,由∠MFN=135°,运用余弦定理可得|MN|,运用抛物线的定义和中位线定理可得d=$\frac{1}{2}$(|MF|+|NF|)=$\frac{1}{2}$(a+b),运用基本不等式计算即可得到所求最小值.
解答 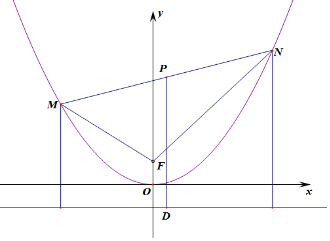 解:抛物线y=4x2的标准方程x2=$\frac{1}{4}$y,则焦点F(0,$\frac{1}{16}$),准线为y=-$\frac{1}{16}$,
解:抛物线y=4x2的标准方程x2=$\frac{1}{4}$y,则焦点F(0,$\frac{1}{16}$),准线为y=-$\frac{1}{16}$,
过P做PD⊥准线l交准线l于D,
设|MF|=a,|NF|=b,由∠MFN=135°,
可得|MN|2=|MF|2+|NF|2-2|MF|•|NF|•cos∠MFN=a2+b2+$\sqrt{2}$ab,
由抛物线的定义可得M到准线的距离为|MF|,N到准线的距离为|NF|,
由梯形的中位线定理可得d=$\frac{1}{2}$(|MF|+|NF|)=$\frac{1}{2}$(a+b),
由|MN|2=λ•d2,可得$\frac{1}{4}$λ=$\frac{{a}^{2}+{b}^{2}+\sqrt{2}ab}{(a+b)^{2}}$=1-$\frac{(2-\sqrt{2})ab}{(a+b)^{2}}$≥1-$\frac{(2-\sqrt{2})ab}{(2\sqrt{ab})^{2}}$=1-$\frac{2-\sqrt{2}}{4}$=$\frac{2+\sqrt{2}}{4}$,
可得λ≥2+$\sqrt{2}$,当且仅当a=b时,取得最小值2+$\sqrt{2}$,
λ的最小值2+$\sqrt{2}$,
故答案为:2+$\sqrt{2}$.
点评 本题考查抛物线的定义、方程和性质,考查余弦定理和基本不等式的运用:求最值,考查化简整理的运算能力,属于中档题.

(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 若f(x)是奇函数,则f(x)是单调函数 | |
| B. | 命题“若x2-x-2=0,则x=1”的逆否命题是“若x≠1,则x2-x-2=0” | |
| C. | 命题p:?x∈R,2x>1024,则¬p:?x0∈R,${2^{x_0}}<1024$ | |
| D. | 命题“?x∈(-∞,0),2x<x2”是真命题 |